
Увод у АНОВА у Р
Следећи чланак АНОВА ин Р даје преглед упоређивања средње вредности различитих група. Анализа варијанце (АНОВА) је врло уобичајена техника која се користи за поређење средње вредности различитих група. АНОВА модел се користи за тестирање хипотеза, где се за претпоставку генерише одређена претпоставка или параметар, а статистички метод се користи за утврђивање да ли је хипотеза тачна или лажна.
Хипотеза је изведена из претпоставке истражитеља и доступних информација о популацији. АНОВА се назива Анализа варијанце и користи се за тестирање хипотеза где се захтева мерење вредности променљиве у више независних група.
На пример, у лабораторији за проучавање или проналазак новог лека за гојазност, истраживачи ће упоредити резултате експерименталног и стандардног лечења. У студији за гојазност могу се добити вредни резултати када се средња стопа гојазности популације може упоредити у различитим старосним групама. У овом случају, желело би се посматрати средња стопа претилости међу различитим старосним групама, као што су узраст (5 до 18), (19, 35) и (36 до 50). АНОВА метода се примењује пошто постоје више од две групе које су независне. АНОВА метода се користи за поређење средње гојазности независних група. Користи се функција аов () и синтакса је аов (формула, дата = датафраме) У овом ћемо чланку научити о АНОВА моделу и даље расправљати о једносмјерном и двосмјерном АНОВА моделу уз примјере.
Зашто АНОВА?
- Ова техника се користи за одговор на хипотезу током анализе више група података. Међутим, постоји више статистичких приступа, АНОВА у Р се примењује када је потребно упоређивање на више од две независне групе, као у нашем претходном примеру три различите старосне групе.
- АНОВА техника мери средину независних група како би истраживачима пружио резултат хипотезе. Да би се добили тачни резултати, морају се узети у обзир средства узорка, величина узорка и стандардно одступање од сваке појединачне групе.
- Средње је могуће посматрати појединачно за сваку од три групе ради поређења. Међутим, овај приступ има ограничења и може се показати нетачним јер ове три поређења не узимају у обзир укупне податке и на тај начин могу довести до грешке типа 1. Р нам пружа функцију за спровођење АНОВА анализе ради испитивања варијабилности међу независним групама података. Постоји пет фаза спровођења АНОВА анализе. У првој фази подаци се сређују у цсв формату и ступац се генерише за сваку променљиву. Један од ступаца била би зависна варијабла, а преостала су независна променљива. У другој фази подаци се читају у Р студију и одговарајуће се називају. У трећој фази, скуп података је прикључен на појединачне променљиве и чита их меморија. Коначно, АНОВА у Р је дефинисана и анализирана. У доњим одељцима пружио сам неколико примера из случаја у којима би требало користити технике АНОВА.
- На 12 поља тестирано је шест инсектицида, а истраживачи су пребројили број бубица који су остали на сваком пољу. Сада фармери морају знати да ли инсектициди имају било какве разлике и ако јесу, који од њих најбоље користе. На ово питање одговорите помоћу функције аов () да бисте извршили АНОВА.
- Педесет пацијената је примило један од пет лекова који смањују холестерол (трт). Три стања лечења укључивала су исти лек који се даје као 20 мг једном дневно (1 пут) 10 мг два пута дневно (2 пута) 5 мг четири пута дневно (4 пута). Два преостала стања (другД и другЕ) представљали су конкурентне лекове. Који третман лековима је донео највеће смањење холестерола (одговор)?
АНОВА једносмерна
- Једносмјерна метода једна је од основних АНОВА техника у којој се примјењује анализа варијанце и успоређује средња вриједност више популацијских група.
- Једносмјерна АНОВА добила је име због доступности једносмерно класификованих података. У једносмјерној АНОВА варијанти и једна или више независних варијабли могу бити доступне.
- На пример, извешћемо АНОВА технику на бази података о холестеролу. Скуп података се састоји од двије варијабле трт (које су третмани на 5 различитих нивоа) и варијабли одговора. Независна варијабла - групе лечења лековима, зависна варијабла - значи 2 или више група АНОВА. Из ових резултата можете потврдити да је узимање доза од 5 мг 4 пута дневно било боље од узимања дозе од двадесет мг једном дневно. Лијек Д има боље ефекте у поређењу с тим лијеком Е
Лек Д даје боље резултате ако се узима у дози од 20 мг у поређењу са леком Е
Користи базу података о холестеролу у пакету с више рачунаinstall.packages('multcomp')
library(multcomp)
str(cholesterol)
attach(cholesterol)
aov_model <- aov(response ~ trt)
АНОВА Ф тест за лечење (трт) је значајан (п <.0001), пружа доказ да је пет третмана
# нису сви једнако ефикасни.
резиме (аов_модел)
одвајање (холестерол)

Функција плотмеанс () у гплотс пакету може се користити за израду графикона групних средстава и њихових интервала поверења Ово јасно показује разлике у третмануinstall.packages('gplots')
library(gplots)
plotmeans(response ~ trt, xlab="Treatment", ylab="Response",
main="Mean Plot\nwith 95% CI")
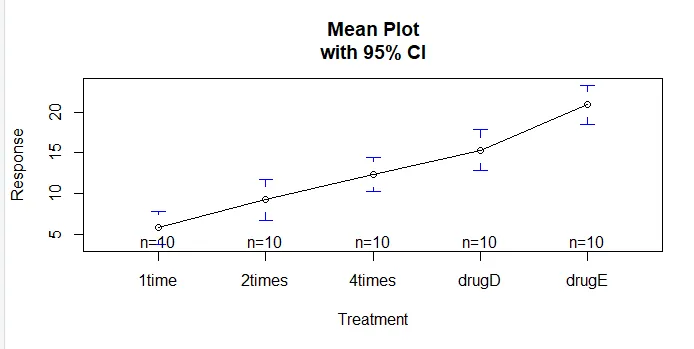
Испитајмо излаз из ТукеиХСД () на парне разлике између групних средстава
ТукеиХСД (аов_модел)
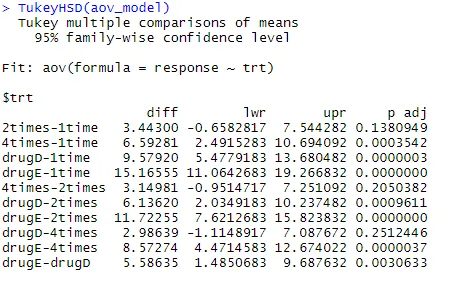
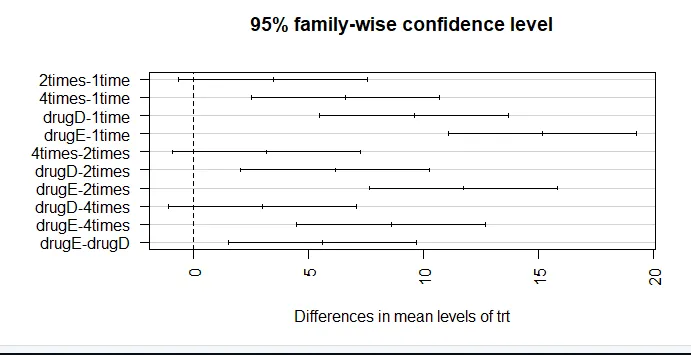
Средње смањење холестерола 1 и 2 пута не разликују се значајно једна од друге (п = 0, 138), док је разлика између 1 и 4 пута значајно различита (п <0, 001).
пар (мар = ц (5, 8, 4, 2)) # повећање гране леве маргине (ТукеиХСД (аов_модел), лас = 2)
Повјерење у резултате овиси о ступњу до којег ваши подаци задовољавају претпоставке на којима се темеље статистички тестови. У једносмјерној АНОВА претпоставља се да је зависна варијабла нормално дистрибуирана и да има једнаку варијанцу у свакој групи. Можете користити КК заплет за процену библиотеке претпоставки о нормалности (аутомобила).
КК заплет (лм (одговор ~ трт, подаци = холестерол), симулира = ТРУЕ, маин = ”КК Плот”, ознаке = ФАЛСЕ)
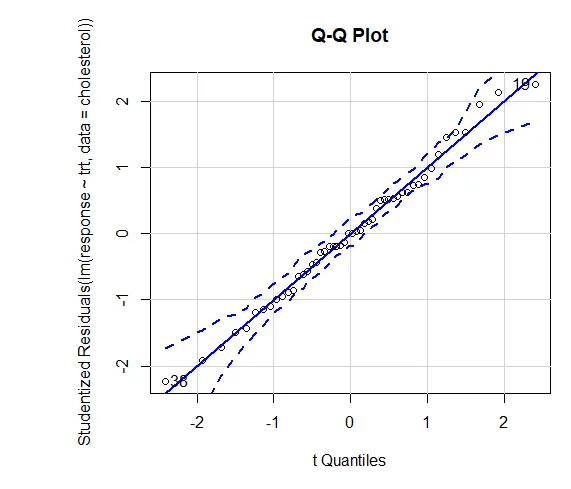
Точкаста линија = коверта поузданости од 95%, што сугерише да је претпоставка о нормалности испуњена прилично добро. АНОВА претпоставља да су одступања једнака у групама или узорцима. Бартлеттов тест се може користити за потврђивање те претпоставке
бартлетт.тест (одговор ~ трт, подаци = холестерол). Бартлеттов тест показује да се одступања у пет група не разликују значајно (п = 0, 97).
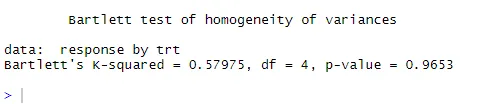
АНОВА је такође осетљива на испитне тестове за аутонименте који користе функцију оутлиерТест () у аутомобилском пакету. Можда нећете требати да покренете овај пакет да бисте ажурирали библиотеку аутомобила.update.packages(checkBuilt = TRUE)
install.packages("car", dependencies = TRUE)
library(car)
outlierTest(aov_model)
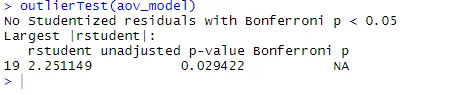
Из резултата се види да у подацима о холестеролу нема назнака за одметнике (НА се јавља када је п> 1). Узимајући КК план, Бартлеттов тест и вањски тест заједно, изгледа да се подаци прилично уклапају у АНОВА модел.
Двосмерна Анова
Још једна варијабла је додата у двосмерном АНОВА тесту. Кад постоје две независне променљиве, мораћемо да користимо двосмерну АНОВА технику, а не једносмерну АНОВА технику која се користила у претходном случају где смо имали једну континуирано зависну променљиву и више од једне независне променљиве. Да би се верификовала двосмерна АНОВА, потребно је удовољити више претпоставки.
- Доступност независних запажања
- Запажања би требало нормално дистрибуирати
- Варијанса треба да буде једнака у опсервацијама
- Остали не треба да буду присутни
- Независне грешке
Да би се верификовала двосмерна АНОВА, скупу података додаје се друга променљива која се зове БП. Варијабла показује стопу крвног притиска код пацијената. Желели бисмо да проверимо да ли постоји статистичка разлика између БП и дозе која се даје пацијентима.
дф <- реад.цсв ("филе.цсв")
дф
анова_тво_ваи <- аов (одговор ~ трт + БП, подаци = дф)
резиме (анова_тво_ваи)
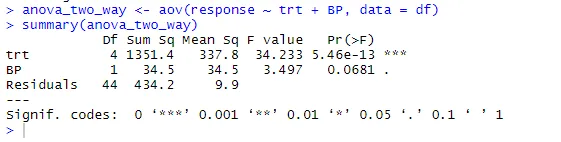
Из резултата се може закључити да се и трт и БП статистички разликују од 0. Према томе, Нулта хипотеза се може одбацити.
Предности АНОВА у Р
АНОВА тестом се одређује разлика између двеју или више независних група. Ова техника је веома корисна за анализу више предмета што је од суштинске важности за анализу тржишта. Употребом АНОВА теста можете добити потребне увиде из података. На пример, током истраживања производа где се од корисника прикупљају више информација, као што су листе за куповину, лајкови купца и несвиђања. АНОВА тест помаже нам да упоредимо групе становништва. Група може бити или Мушкарац вс Жена или различите старосне групе. АНОВА техника помаже у разликовању средњих вриједности различитих група становништва које су заиста различите.
Закључак - АНОВА у Р
АНОВА је једна од најчешће коришћених метода за тестирање хипотеза. У овом чланку смо урадили АНОВА тест на скупу података који се састојао од педесет пацијената који су примили лек за смањење холестерола и даље видели како се двосмерна АНОВА може извести када је на располагању додатна независна варијабла.
Препоручени чланци
Ово је водич за АНОВА у Р. Овде смо расправљали о једносмерном и двосмерном Анова моделу заједно са примерима и предностима АНОВА-е. Можете и да прођете кроз друге наше предложене чланке -
- Регрессион вс АНОВА
- Шта је СПСС?
- Како тумачити резултате користећи АНОВА тест
- Функције у Р