Увод у хијерархијско кластерирање
- Недавно је један од наших клијената тражио од нашег тима да изнесе списак сегмената по редоследу важности за своје купце, како би их усмерио у франшизу једног од својих нових производа. Јасно је да само сегментирање купаца коришћењем делимичног кластерирања (к-значи, ц-фуззи) неће донијети важан редослед тамо где хијерархијско кластерирање улази у слику.
- Хијерархијско кластерирање раздваја податке у различите групе на основу неких мера сличности познатих као кластери, а који у основи циља на изградњу хијерархије међу кластерима. У основи је неконтролирано учење и одабир атрибута за мјерење сличности је специфичан за примјену.
Кластер хијерархије података
- Агломеративно кластерирање
- Подељено кластерирање
Узмимо за пример податке, оцене које је добило 5 ученика како бисмо их груписали за предстојеће такмичење.
| Ученик | Оцене |
| А | 10 |
| Б | 7 |
| Ц | 28 |
| Д | 20 |
| Е | 35с |
1. Агломеративно кластерирање
- За почетак размотримо сваку појединачну тежину тачке / елемента овде као кластере и настављамо спајањем сличних тачака / елемената да би формирали нови кластер на новом нивоу све док нам појединачни кластер не остане приступ одоздо према горе.
- Појединачна и потпуна веза два су популарна примјера агломеративног групирања. Осим ове Просечне везе и Центроидне везе. У једном повезивању, у сваком кораку спајамо два кластера, чија два најближа члана имају најмању удаљеност. У потпуном повезивању спајамо се у чланове најмањег растојања који пружају најмању максималну удаљеност између пара.
- Матрица близине, То је језгро за обављање хијерархијских кластерирања, које дају удаљеност између сваке тачке.
- Направимо матрицу близине за наше податке дате у табели, јер израчунавамо растојање сваке тачке са осталим тачкама, то ће бити асиметрична матрица облика н × н, у нашем случају 5 × 5 матрица.
Популарна метода за израчунавање растојања је:
- Еуклидијска удаљеност (у квадрату)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Манхаттан дистанце
dist((x, y), (a, b)) =|x−c|+|y−d|
Еуклидијска удаљеност се најчешће користи, ту ћемо је користити и ићи ћемо сложеним повезивањем.
| Студент (кластери) | А | Б | Ц | Д | Е |
| А | 0 | 3 | 18 | 10 | 25 |
| Б | 3 | 0 | 21 | 13 | 28 |
| Ц | 18 | 21 | 0 | 8 | 7 |
| Д | 10 | 13 | 8 | 0 | 15 |
| Е | 25 | 28 | 7 | 15 | 0 |
Дијагонални елементи матрице за близину увек ће бити 0, јер ће удаљеност између тачке са истом тачком увек бити 0, стога су дијагонални елементи изузети из разматрања за груписање.
Овде је у итерацији 1 најмања удаљеност 3, стога спајамо А и Б у формирање кластера, поново формирамо нову матрицу близине са кластером (А, Б), узимајући (А, Б) тачку кластера као 10, тј. Максимално ( 7, 10) тако би била новоформирана матрица близине
| Кластери | (А, Б) | Ц | Д | Е |
| (А, Б) | 0 | 18 | 10 | 25 |
| Ц | 18 | 0 | 8 | 7 |
| Д | 10 | 8 | 0 | 15 |
| Е | 25 | 7 | 15 | 0 |
У итерацији 2, 7 је минимална удаљеност стога спајамо Ц и Е формирајући нови кластер (Ц, Е), понављамо поступак који следи у итерацији 1 док не завршимо са једним кластером, овде се заустављамо на итерацији 4.
Читав поступак је приказан на слици испод:
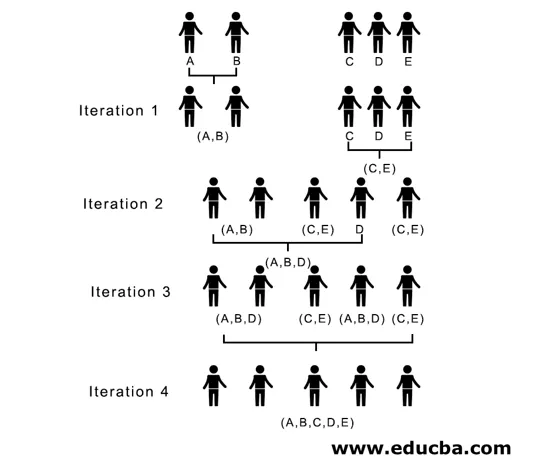
(А, Б, Д) и (Д, Е) су два кластера формирана у итерацији 3, на последњој итерацији коју видимо можемо да останемо са једним кластером.
2. Дивисивна кластеризација
За почетак сматрамо све тачке јединственим групом и раздвајамо их на најудаљенију раздаљину док појединачне тачке не завршимо као појединачне групе (не нужно да се можемо зауставити у средини, зависи од минималног броја елемената које желимо у сваком кластеру) на сваком кораку. То је управо супротно агломеративном удруживању и то је приступ одозго према доле. Подељено кластерирање је начин на који се понавља к значи груписање.
Избор између агломеративног и подељеног кластерирања поново зависи од апликације, али треба узети у обзир неколико тачака:
- Подјела је сложенија од агломеративног групирања.
- Подељено кластерирање је ефикасније ако не створимо потпуну хијерархију до појединих тачака података.
- Агломеративно удруживање доноси одлуку узимајући у обзир локалне узорке, не узимајући у обзир глобалне обрасце који се у почетку не могу преокренути.
Визуализација хијерархијског кластерирања
Супер корисна метода за визуелизацију хијерархијског групирања која помаже у пословању је Дендограм. Дендограми су структуре налик на дрвеће које бележе редослед спајања и расцепа у којима вертикална линија представља удаљеност између кластера, удаљеност између вертикалних линија и удаљеност између кластера је директно пропорционална, односно већа је удаљеност што су кластери вероватно различити.
Помоћу дендограма можемо одредити број кластера, само цртамо линију која се пресече са најдужом вертикалном линијом на дендограму, број вертикалних линија које су пресечене биће број кластера који се узимају у обзир.
Испод је пример Дендограм.
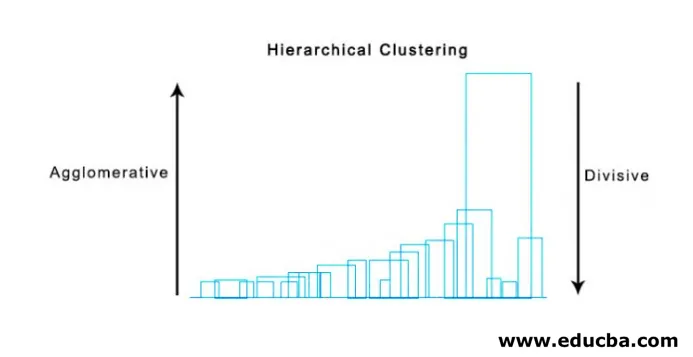
Постоје прилично једноставни и директни питхон пакети и његове функције за извршавање хијерархијског кластерирања и цртање дендограма.
- Хијерархија науке.
- Цлустер.хиерарцхи.дендограм за визуелизацију.
Уобичајени сценарији у којима се користи хијерархијско кластерирање
- Сегментација корисника на маркетинг производа или услуга.
- Градско планирање да идентификује места за изградњу структура / услуга / зграда.
- Анализа друштвених мрежа, на пример, идентификује све обожаватеље МС Дхони-а да рекламирају његов биопиц.
Предности хијерархијског кластерирања
Предности су дате у наставку:
- У случају дјеломичног групирања попут к-средстава, број кластера треба бити познат прије кластерирања, што није могуће у практичним апликацијама, док у хијерархијском кластерирању није потребно претходно знање броја кластера.
- Хијерархијско кластерирање производи хијерархију, тј. Структуру информативнију од неструктурираног скупа равних кластера враћених дјеломичним кластерирањем.
- Хијерархијско кластерирање је лако имплементирати.
- Доноси резултате у већини сценарија.
Закључак
Тип кластерирања доноси велику разлику када се подаци презентују, више је пожељно хијерархијско кластерирање које је информативније и лако је анализирати него делимично кластерирање. А често је повезана са топлотним мапама. Да се не забораве атрибути одабрани за израчунавање сличности или различитости, који претежно утичу и на кластере и на хијерархију.
Препоручени чланци
Ово је водич за хијерархијско кластерирање. Овдје ћемо разговарати о уводу, предностима хијерархијског кластерирања и уобичајеним сценаријима у којима се користи хијерархијско кластерирање. Можете и да прођете кроз друге наше предложене чланке да бисте сазнали више -
- Алгоритам кластера
- Кластерирање у машинском учењу
- Хијерархијско кластерирање у Р
- Методе кластерирања
- Како уклонити хијерархију у Таблеау-у?