
Увод у Фибонаццијеве серије у Питхону
Фибонаццијева серија у Питхону, ово се назива низом бројева, при чему је следећи број збир двају бројки.
На пример:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. тако даље
Дакле, овде 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 и тако даље.
Гледајући горе наведено, могло би се добити одређена идеја о чему причамо.
Међутим, у смислу математичког правила, може се написати као:

Где је н-ти број зброј броја на местима (н-1) и (н-2). Када је у питању имплементација Фибонаццијеве серије, могао би бити већи број језика кодирања путем којих би се то могло учинити.
Међутим, Питхон је данас широко кориштен језик. Погледајмо имплементацију Фибонаццијеве серије кроз Питхон. Требало би бити свестан основних изјава о условљавању, као што су петља, ако не, док је петља итд. На Питхон-у, пре него што наставите овде. Ако не, било би сјајно ако га неко може ревидирати, а затим преузима надолазећи садржај. Овде у демо сврху користим шпијун који је ИДЕ за програмски језик питхон-а. Можете користити било које друге ИДЕ или Ипитхон нотебоок рачунаре као и за извршавање Питхон програма.
Фибонаццијева серија у Питхону
Погледајмо имплементацију Фибонаццијевих броја и серија узимајући у обзир прва два елемента Фибонације су 0 и 1:
Међутим, можете прилагодити функцију Фибонацција према вашим захтевима, али прво сагледати основе и постепено прећи на друге.
Питхон код за проналажење н-ог Фибонаццијевог броја
Шифра 1:
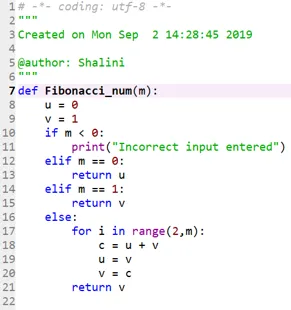
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Шифра 2:
Излаз:
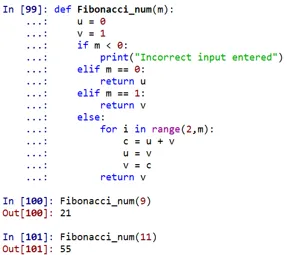
Као што се може видети, Фибонаццијев број на 9. месту био би 21, а на 11. месту 55.
- Овде је означена „функција_нум“ дефинисана је функција која води рачуна о проналажењу Фибонаццијевог броја уз помоћ одређених услова. Ову функцију можете позвати навођењем било којег положаја.
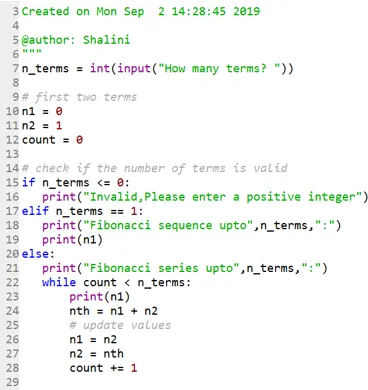
Сада да видимо како се могу штампати серије до поменуте позиције:
Шифра:
Излаз:
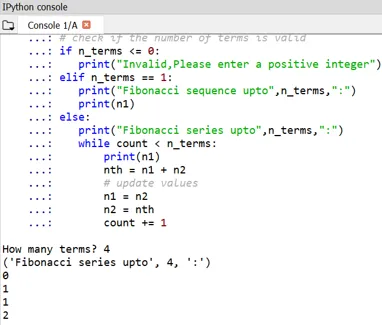
Може се приметити да је почетак Фибонаццијевих бројева дефинисан као 0 и 1.
- Ако неко жели дефинирати властите почетне појмове, то се може учинити на исти начин подешавањем н1 и н2. Ево примера за то:
Рецимо сада да желимо да наши почетни услови буду: н1 = 3, н2 = 5
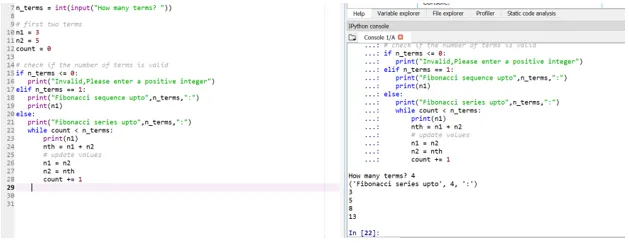
Дакле, овде ће се одлучити о вашем четверогодишњем положају (кориснички унос), на основу ваших почетних услова.
Методе помоћу којих се може створити Фибонаццијева серија
Испод су три методе помоћу којих се могу створити Фибонаццијеве серије:
1. Кроз Генераторе
Шифра:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Излаз:
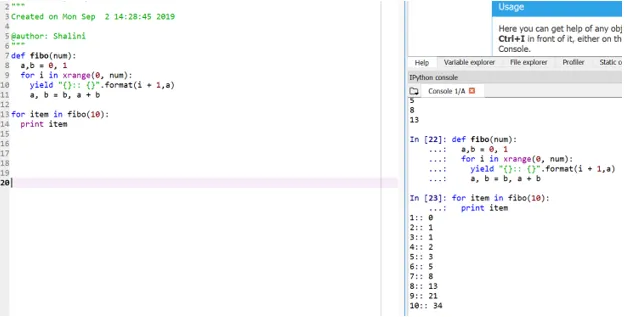
Ова метода се назива "генератор", јер је функција кранге генератор бројева између 0 и броја, а принос је генератор за форматирани излаз.
Ево шта кранге ради за вас:

Овде је Фибонаццијева серија дефинисана у облику функције, унутар које се за излаз брине функција петље, кранге и приноса.
2. Кроз петљу
Шифра:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Излаз:

Као што се види, за штампање Фибонаццијеве серије између 0 и 10. кориштен је једноставан за петљу, а унутра су за променљиве додељене нове вредности. У и в су задане почетне вредности Фибонацције које су постављене на 0 и 1 респективно.
Што се тиче кретања петље, нова вредност у је стара вредност в, док је нова вредност в сума старих вредности у и в. То се наставља до краја вредности опсега.
3. Кроз рекурзију
Шифра:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Излаз:
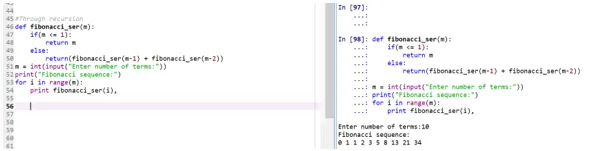
- Функција „Веигхт_сер“ упућује позив себи да штампа Фибонаццијеву серију.
- И отуда је метода добила име "рекурзија".
Следећи кораци:
- Овде се од корисника тражи да унесе место на коме ће бити одштампан Фибонаццијев низ.
- Бројка пролази кроз функцију „вредјача“.
- Услов се провјерава, ако је наведена дужина мања од 1 или не. Ако је одговор да, резултат се даје одмах.
- Међутим, ако је дужина већа од 1, упућују се рекурзивни позиви на „вредан_сер" са аргументима дужине мањом од 1 и 2, тј.
- Дакле, рекурзија даје жељени излаз и штампа га.
- Дакле, укратко, Размотрили смо три начина за приказивање Фибонаццијеве серије.
- Кроз петљу, генераторе и рекурзију.
Сва три Питхон кода су сумирана
Испод су три питхон кода:
1. Кроз Генераторе
Шифра:
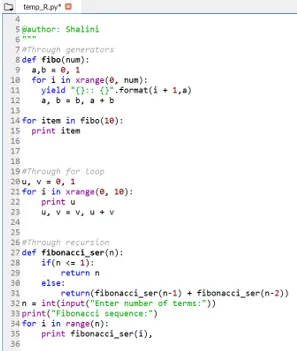
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Кроз петљу
Шифра:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Кроз рекурзију
Шифра:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Горе сажето су све процедуре, потребно је вежбати да бисте се добро ухватили за све.
Излаз:
Закључак
Пролазећи кроз горњи садржај Фибонација, човек би имао кристално јасно разумевање Фибонаццијевих бројева и серија, специјализованих са питоном. Једном, неко се удовољи логици Фибонаццијеве серије, генерисање другог низа серија, рад са другим бројевима и разним методама сада ће бити прави потез за вас. Логички приступ је једини начин да се то постигне.
Препоручени чланци
Ово је водич за Фибонаццијеве серије у Питхону. Овде смо разговарали о Фибонаццијевим бројевима и серијама, специјализованим за питхон, генерисањем другог скупа серија, радом са другим бројевима и разним методама. Можете и да прођете кроз остале сродне чланке да бисте сазнали више -
- Генератор случајних бројева у Питхон-у
- Математичке функције у Питхон-у
- Факторориал у Питхон-у
- Инкапсулација у Питхон-у
- Серија Фибонацције на Јави
- Особине Питхон-а
- Факторски програм у ЈаваСцрипт-у
- Генератор случајних бројева у Матлабу
- Генератор случајних бројева у Ц #
- Инкапсулација у ЈаваСцрипт-у