Разлика између линеарне регресије и логистичке регресије
Следећи чланак Линеарна регресија вс логистичка регресија пружа најважније разлике између оба, али пре него што ћемо видети шта значи регресија?
Регресија
Регресија је у основи статистичка мјера којом се утврђује јачина везе између једне зависне варијабле, тј. Излаза И и низа других независних варијабли, тј. Кс 1, Кс 2 и тако даље. Регресијска анализа се у основи користи за предвиђање и предвиђање.
Шта је линеарна регресија?
Линеарна регресија је алгоритам који се заснива на домену машинског учења под надзором учења. Она насљеђује линеарни однос између својих улазних варијабли и појединачне излазне варијабле гдје је излазна варијабла у природи континуирана. Користи се за предвиђање вредности излаза, рецимо И из улаза, рецимо Кс. Када се сматра само један улаз назива се једноставном линеарном регресијом.
Може се сврстати у две главне категорије:
1. Једноставна регресија
Принцип рада: Главни циљ је пронаћи једнаџбу равне линије која најбоље одговара узоркованим подацима. Ова једначина алгебрично описује однос између две променљиве. Равна линија која најбоље пристаје назива се регресијска линија.
Y = β 0 + β 1 X
Где,
β представља карактеристике
β 0 представља пресретање
β 1 представља коефицијент карактеристике Кс
2. Мултиваријабилна регресија
Користи се за предвиђање корелације између више независних променљивих и једне зависне променљиве. Регресија са више од две независне променљиве заснива се на уклапању облика у сазвежђе података на вишедимензионалном графу. Облик регресије треба да буде такав да умањује удаљеност облика од сваке тачке података.
Модел линеарног односа може се математички представити на следећи начин:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Где,
β представља карактеристике
β 0 представља пресретање
β 1 представља коефицијент карактеристике Кс1
β н представља коефицијент карактеристике Кс н
Предности и недостаци линеарне регресије
Испод су наведене предности и недостаци:
Предности
- Због своје једноставности, широко се користи моделирање за предвиђања и закључке.
- Усредсређен је на анализу података и предобраду података. Дакле, бави се различитим подацима без муке око детаља модела.
Недостаци
- Дјелује ефикасно када се подаци нормално дистрибуирају. Стога се за ефикасно моделирање мора избегавати колинеарност.
Шта је логистичка регресија?
То је облик регресије који омогућава предвиђање дискретних варијабли мешавином континуираних и дискретних предиктора. Резултат је јединствена трансформација зависних променљивих која утиче не само на процену процене већ и на коефицијенте независних променљивих. Бави се истим питањем које има вишеструка регресија, али без дистрибутивних претпоставки о предикторима. У логистичкој регресији варијабла исхода је бинарна. Сврха анализе је проценити ефекте више објашњивих променљивих, које могу бити нумеричке или категоричке или обоје.
Врсте логистичке регресије
Испод су наведене две врсте логистичке регресије:
1. Бинарна логистичка регресија
Користи се када је зависна варијабла дихотомна тј. Попут дрвета са две гране. Користи се када је зависна варијабла непараметарска.
Користи се када
- Ако нема линеарности
- Постоје само два нивоа зависне променљиве.
- Ако је мултиваријантна нормалност упитна.
2. Мултиномална логистичка регресија
Мултиноминална логистичка регресијска анализа захтева да независне променљиве буду метричке или дихотомне. Не даје никакве претпоставке о линеарности, нормалности и хомогености варијанце за независне променљиве.
Користи се када зависна варијабла има више од две категорије. Користи се за анализу односа између не метричке зависне променљиве и метричких или дихотомских независних променљивих, а затим упоређује више група комбинацијом бинарних логистичких регресија. На крају, он пружа скуп коефицијената за сваку од две поређења. Коефицијенти за референтну групу су све нуле. Коначно, предвиђање се врши на основу највеће резултатске вероватноће.
Предност логистичке регресије: То је врло ефикасна и широко коришћена техника јер не захтева много рачунских ресурса и не захтева подешавање.
Недостатак логистичке регресије: Не може се користити за решавање нелинеарних проблема.
Упоређивање између линеарне регресије и логистичке регресије (Инфограпхицс)
Испод је топ 6 разлике између линеарне регресије и логистичке регресије 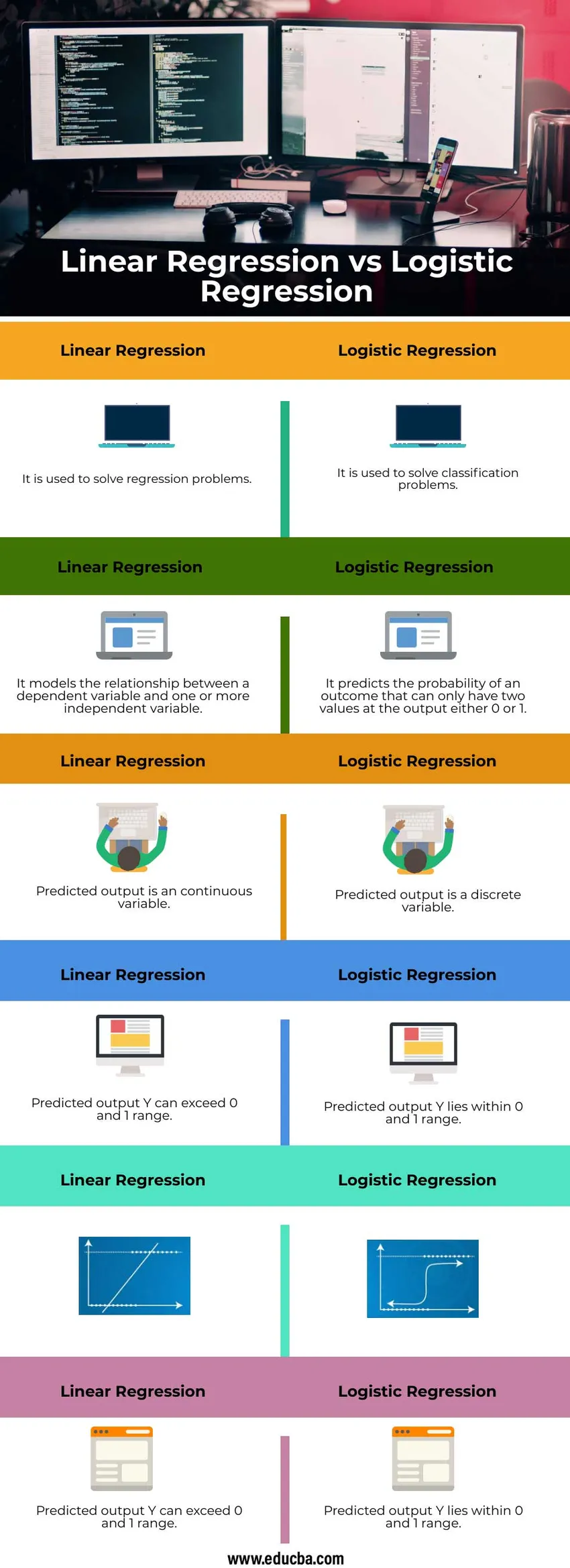
Кључна разлика између линеарне регресије и логистичке регресије
Расправимо о неким главним кључним разликама између линеарне регресије и логистичке регресије
Линеарна регресија
- То је линеарни приступ
- Користи равну линију
- Не може да преузме категоричке променљиве
- Мора да игнорише запажања са недостајућим вредностима нумеричке независне променљиве
- Излаз И је дат као
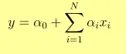
- Повећање за 1 јединицу к повећава И за α
Апликације
- Предвиђање цене производа
- Предвиђање резултата на утакмици
Логистичка регресија
- То је статистички приступ
- Користи сигмоидну функцију
- Може да преузме категоричке променљиве
- Може да доноси одлуке чак и ако постоје запажања са недостајућим вредностима
- Излаз И је дат као, где је з дан као
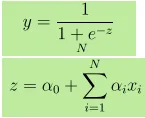
- Повећање за 1 јединицу у к повећава И одбором од α
- Ако је П вероватноћа неког догађаја, тада је (1-П) вероватноћа да се он неће догодити. Шансе за успех = П / 1-П
Апликације
- Предвиђање да ли ће данас киша или не.
- Предвиђање да ли је е-пошта нежељена пошта или не.
Табела упоређивања линеарне регресије и логистичке регресије
Разговарајмо о горњем поређењу између линеарне регресије и логистичке регресије
|
Линеарна регресија |
Логистичка регресија |
| Користи се за решавање регресијских проблема | Користи се за решавање проблема класификације |
| Она моделира однос између зависне променљиве и једне или више независних променљивих | Предвиђа вероватноћу исхода која на излазу може имати само две вредности било 0 или 1 |
| Предвиђени излаз је континуирана променљива | Предвиђени излаз је дискретна варијабла |
| Предвиђени излаз И може прећи опсег 0 и 1 | Предвиђени излаз И лежи унутар 0 и 1 опсега |
 | 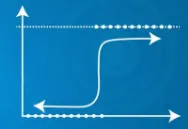 |
| Предвиђени излаз И може прећи опсег 0 и 1 | Предвиђени излаз |
Закључак
Ако функције не доприносе предвиђању или су у великој корелацији једна са другом, онда моделу додаје буку. Дакле, карактеристике које не доприносе довољно моделу морају бити уклоњене. Ако су независне варијабле високо повезане, то може изазвати проблем мултиколинеарности, што се може решити покретањем засебних модела са сваком независном променљивом.
Препоручени чланци
Ово је водич за Линеарну регресију и логистичку регресију. Овде смо размотрили кључне разлике линеарне регресије и логистичке регресије са инфографиком и упоредном табелом. Можда ћете такође погледати следеће чланке да бисте сазнали више -
- Дата Сциенце вс визуализација података
- Машинско учење и неуронска мрежа
- Надзирано учење вс Дубоко учење
- Логистичка регресија у Р