
Увод у биномну дистрибуцију у Р
Овај чланак описује како се користе биномне дистрибуције у Р за неколико операција укључених у дистрибуцију вероватноће. Пословна анализа користи биномну вероватноћу за сложен проблем. Р има бројне уграђене функције за израчунавање биномних дистрибуција које се користе у статистичким сметњама. Биномна дистрибуција позната и као Берноуллијева испитивања узима двије врсте успјеха п и неуспјеха С. Главни циљ модела биномне дистрибуције је израчунавање могућих исхода вјероватноће надгледањем одређеног броја позитивних могућности понављањем поступка одређени број пута . Они би требали имати два могућа резултата (успјех / неуспјех), па је исход дволичан. Унапред дефинисани математички запис је п = успех, к = 1-п.
Постоје четири функције повезане са биномним расподелбама. Они су дбином, пбином, кбином, рбином. Форматирана синтакса је дата у наставку:
Синтакса
- дбином (к, величина, проба)
- пбином (к, величина, проб)
- кбином (к, сизе, проб) или кбином (к, сизе, проб, ловер_таил, лог_п)
- рбином (к, величина, проб)
Функција има три аргумента: вредност к је вектор квантила (од 0 до н), величина је број покушаја стаза, проба означава вероватноћу за сваки покушај. Погледајмо један по један пример.
1) дбином ()
То је функција густине или дистрибуције. Вриједности вектора морају бити цијели број, не смије бити негативан број. Ова функција покушава пронаћи број успеха у не. суђења која су фиксна.
Биномна расподјела узима величину и к вриједности. на пример, величина = 6, могуће вредности к су 0, 1, 2, 3, 4, 5, 6 што имплицира П (Кс = к).
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Излаз:
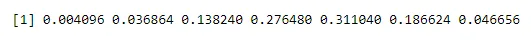
Успостављање вероватноће за један
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Излаз:
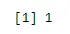
Пример 1 - Болничка база података показује да пацијенти који пате од рака 65% умиру од њега. Колика ће бити вероватноћа да ће 5 насумично изабраних пацијената од којих ће се 3 опоравити?
Овде примењујемо функцију дбином. Вероватноћа да ће се 3 опоравити користећи расподелу густине у свим тачкама.
н = 5, п = 0, 65, к = 3
dbinom(3, size=5, prob=0.65)
Излаз:

За к вредност 0 до 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Излаз:
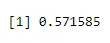
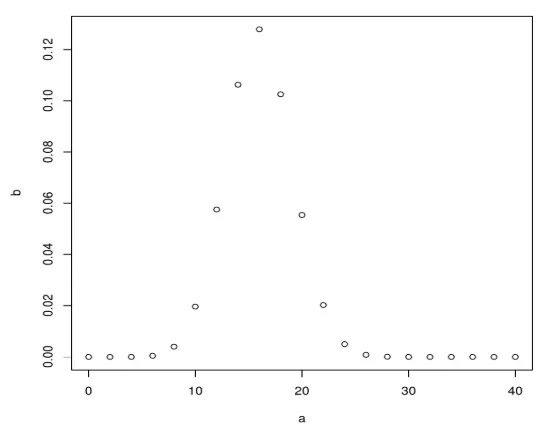
Затим направите узорак од 40 папира и повећајте за 2 такође креирајући бином помоћу дбинома.
a <- seq(0, 40, by = 2)
b <- dbinom(a, 40, 0.4)
plot(a, b)
Након извршења горњег кода ствара следећи излаз: Биномна дистрибуција се црта помоћу функције плот ().
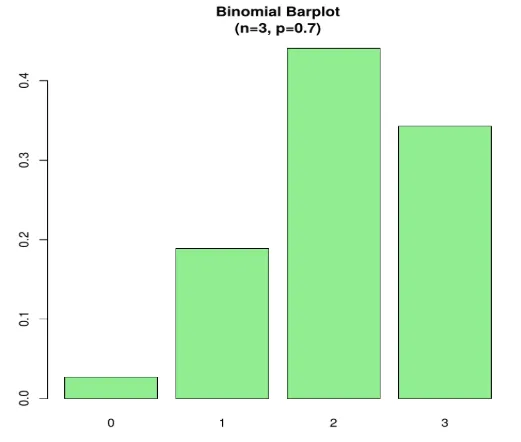
Пример 2 - Узмимо у обзир сценарио, претпоставимо да је вероватноћа да ће студент позајмити књигу из библиотеке 0, 7. У библиотеци има 6 ученика, колика је вероватноћа да ће 3 њих позајмити књигу?
овде П (Кс = 3)
Шифра:
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Испод графикона приказује се када је п> 0, 5, па је биномна дистрибуција позитивно нагнута као приказана.
Излаз:
2) Пбином ()
израчунава кумулативне вероватноће биномних или ЦДФ (П (Кс <= к)).
Пример 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Излаз:

Пример 2: Дравид постигне ветрицу на 20% својих покушаја када кугла. Ако се кугла 5 пута, колика би била вероватноћа да ће забити 4 или мањи велет?
Вероватноћа успеха је овде 0.2 и током 5 покушаја које добијамо
pbinom(4, size=5, prob=.2)
Излаз:
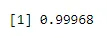
Пример 3: 4% Американаца су црнци. Пронађите вјероватноћу 2 црначка ученика случајним одабиром 6 ученика из разреда 100 без замјене.
Када је Р: к = 4 Р: н = 6 Р: п = 0. 0 4
pbinom(4, 6, 0.04)
Излаз: -
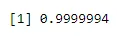
3) кбином ()
То је квантитативна функција и врши инверзију функције кумулативне вероватноће. Кумулативна вредност се подудара са вероватноћом вероватноће.
Пример: Колико ће репова имати вероватноћу 0, 2 када се новчић баци 61 пута.
a <- qbinom(0.2, 61, 1/2)
print(a)
Излаз: -
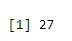
4) рбином ()
Он генерише случајне бројеве. Различити исходи дају различите случајне резултате, кориштене у процесу симулације.
Пример: -
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Излаз: -

Сваки пут када га извршимо даје случајне резултате.
rbinom(200, 4, 0.4)
Излаз: -

Ово радимо тако што претпостављамо исход 30 окретаја новчића у једном покушају.
rbinom(30, 1, 0.5)
Излаз: -
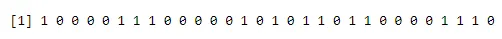
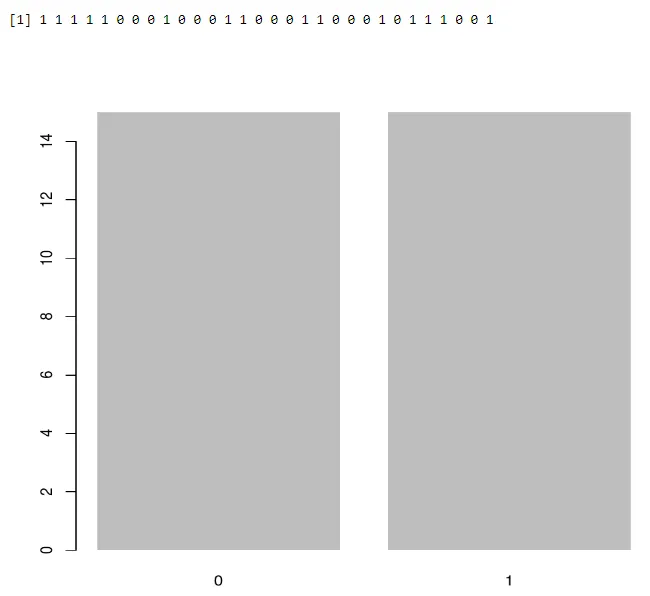
Коришћење барплота:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Излаз: -
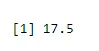
Да пронађете средину успеха
output <-rbinom(10, size=60, 0.3)
mean(output)
Излаз: -
Закључак - Биномна дистрибуција у Р
Дакле, у овом документу смо расправљали о биномној дистрибуцији у Р. Симулирали смо користећи различите примере у Р студију и Р исечцима и такође описали уграђене функције које помажу у генерисању биномних израчуна. Израчун биномне дистрибуције у Р користи статистичке прорачуне. Стога, биномна дистрибуција помаже у проналажењу вјероватности и случајном претраживању користећи биномну варијаблу.
Препоручени чланци
Ово је водич за биномну дистрибуцију у Р. Овде смо расправљали о уводу и његовим функцијама повезаним са биномном дистрибуцијом, заједно са синтаксом и одговарајућим примерима. Можете и да прођете кроз друге наше предложене чланке да бисте сазнали више -
- Формула биномне дистрибуције
- Економија вс бизнис
- Технике пословне аналитике
- Линук дистрибуције