Формула ефективне годишње стопе (Садржај)
- Формула
- Примери
- Калкулатор
Шта је ефективна годишња формула формуле?
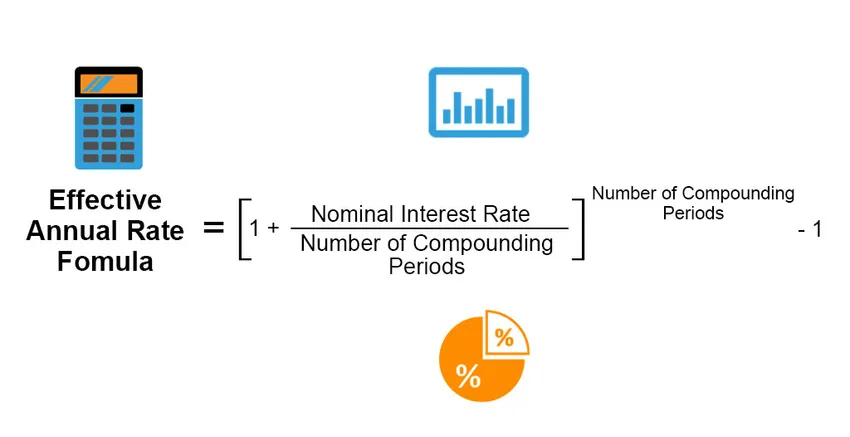
Ефективна годишња стопа је стварна каматна стопа која се зарађује или исплаћује на инвестицији, зајму или било ком сличном финансијском производу, а разликује се од „номиналне каматне стопе“ због периода исплате камате, сложености каматне стопе, укупне временски период зајма или инвестиције итд. Ефективна годишња стопа се израчунава следећом формулом;
Effective Annual Rate = ((1 + (Nominal Interest Rate / Number of Compounding Periods)) Number of Compounding Periods) – 1
Примери формула ефективне годишње стопе (са Екцеловим предлошком)
Узмимо пример да бисмо боље разумели израчунавање ефективне годишње стопе.
Овде можете преузети овај ефективни образац за образац ефективне годишње стопе овде - Образац ефективне годишње формула формула ЕкцелФормула ефективне годишње стопе - Пример бр. 1
Претпоставимо да господин Кс узима лични кредит од банке са каматном стопом од 20%, сложени полугодишње. Израчунајте ефективну годишњу стопу користећи информације.

Решење:
Ефективна годишња стопа се израчунава према доњој формули
Ефективна годишња стопа = ((1 + (Номинална каматна стопа / Број спојних периода)) Број спојних периода) - 1

- Ефективна годишња стопа = ((1 + (20% / 2)) 2) - 1
- Ефективна годишња стопа = 21%
Формула ефективне годишње стопе - Пример бр. 2
Претпоставимо да је господин А уложио 100 УСД у депозитни сертификат који исплаћује номиналну годишњу каматну стопу од 10% која се сачињава на кварталној основи. Израчунајте ефективну годишњу стопу.

Решење:
Ефективна годишња стопа се израчунава према доњој формули
Ефективна годишња стопа = ((1 + (Номинална каматна стопа / Број спојних периода)) Број спојних периода) - 1
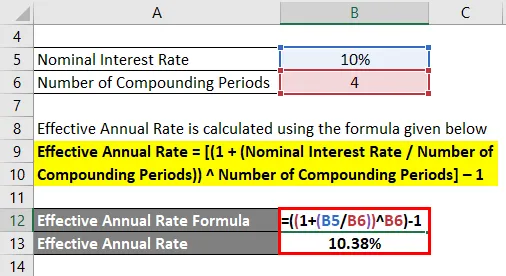
- Ефективна годишња стопа = ((1 + (10% / 4)) 4) - 1
- Ефективна годишња стопа = 10, 38%
Формула ефективне годишње стопе - Пример бр. 3
Претпоставимо да улагање у узајамни фонд узима 15, 50% годишње каматне стопе као зараде, док П2П позајмљивање зарађује 15% годишње номиналне стопе камате, сложено месечно. Стога израчунајте ефективну годишњу стопу за оба случаја.

Решење:
Ефективна годишња стопа се израчунава према доњој формули
Ефективна годишња стопа = ((1 + (Номинална каматна стопа / Број спојних периода)) Број спојних периода) - 1
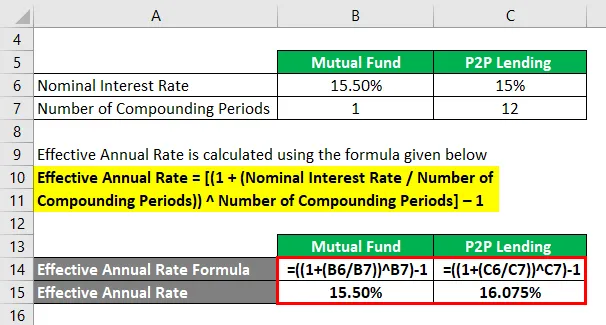
За узајамни фонд
- Ефективна годишња стопа = ((1 + (15, 50% / 1)) 1) - 1
- Ефективна годишња стопа = 15, 50%
За П2П позајмљивање
- Ефективна годишња стопа = ((1 + (15% / 12)) 12) - 1
- Ефективна годишња стопа = 16.075%
Објашњење
Номинална каматна стопа је исказана стопа на финансијски производ. У примјеру 3, номинална стопа приказана на производе чини да узајамни фонд изгледа као преферирани избор улагања за инвеститоре због 0, 50% веће годишње номиналне стопе камате.
Међутим, ефективна годишња стопа израчунава се узимајући номиналну годишњу каматну стопу и састављајући је за одређени период (12 ако је сједињење месечно; 6 ако је сједињење двомјесечно; 4 ако је тромјесечно; 2 ако је је полугодишња) примењива у временском распону од једне године. У случају узајамног фонда, број периода компонирања годишње је 1, док је у случају П2П позајмљивања месечно, па отуда постоји 12 периода сједињења.
На основу формуле,
Ефективни годишњи поврат = ((1 + (номинална каматна стопа / број периода компоновања)) (број периода компоновања) - 1
Ефективни годишњи повраћај узајамног фонда = ((1 + (15, 50% / 1)) 1) - 1 = 15, 50%
П2П ефективни годишњи поврат = ((1 + (15.00% / 12)) 12) - 1 = 16.075%
Релевантност и употреба ефективне формуле годишње стопе
Формула ефективне годишње стопе користи се за разликовање стварног ИРР-а (унутрашња стопа приноса) или годишњег приноса за каматну стопу која се може или не мора сложити више пута током одређеног периода. Ово би се могло веома добро употријебити за упоређивање различитих врста могућности улагања или зајамних кредита узетих у оквиру различитих структура.
Претпоставимо да постоје две могућности улагања, орочени орочени депозити и фиксни депозити банке на које се инвеститор сузио, узимајући у обзир његов / њен апетит за ризиком и погодност. Крајњи циљ инвеститора је да максимално искористи ове депозите и оствари већи принос. Међутим, оба инструмента нуде мало различите каматне стопе, док орочени депозит у Поштама нуди тромјесечно поравнање за предметни термин.
- Износ улагања: Рс 10 лакхс
- Период улагања: 5 година
- Фиксни депозит у банци: 7, 5% годишње камате
- Орочени депозит на поштама: 7, 4% годишње камате, сложен квартално
По изгледу понуђених годишњих каматних стопа, чини се да је фиксни депозит у банци боља опција. Међутим, ако инвеститор заиста израчуна квартални фактор слагања депозита на поштанској пошти, то резултира ефективном годишњом стопом / повратом од 7, 61%.
Због ове мале промене са ефективне стопе од 7, 4% до 7, 61%, инвеститор би зарадио укупно Рс. 4, 42, 848.28 од овог конкретног инструмента, док би он / она зарадили Рс. 3, 35, 469.14 од инструмента Банке са фиксним депозитом.
Ако инвеститор пропусти израчунавање ове ефективне годишње стопе, изгубио би прилику да добије отприлике више од Рс. 1 лакх од његове инвестиције.
Калкулатор ефективне годишње стопе
Можете да користите следећи калкулатор ефективне годишње стопе
| Номинална каматна стопа | |
| Број сложених периода | |
| Ефективна годишња стопа | |
| Ефективна годишња стопа = | ((1 + (Номинална каматна стопа / Број спојних периода)) Број спојних периода ) - 1 | |
| ((1 + (0/0)) 0 ) - 1 = | 0 |
Препоручени чланци
Ово је водич за Формулу ефективне годишње стопе. Овде смо расправљали о начину израчуна ефективне годишње стопе заједно са практичним примерима. Такође пружамо ефективни годишњи калкулатор за рате с могућношћу скидања екцел предлошка. Такође можете погледати следеће чланке да бисте сазнали више -
- Калкулатор за формулу реалне каматне стопе
- Формула за повраћај капитала запосленог | Дефиниција
- Како израчунати ефективну каматну стопу?
- Шта је садашња вредност формуле ануитета?