СИН функција у Екцелу - Како се користи СИН функција у Екцелу?

Екцел СИН функција (Садржај)

• СИН функција у Екцелу
• Како се користи СИН функција у Екцелу?

СИН функција у Екцелу

Способност израчунавања не обухвата целокупност математике. То је његов пододјељак, иако пресудан у његовој примјени. У годинама које су пролазиле то је био ограничавајући фактор, изузев много познатих и надасве талентованих "људских калкулатора", као што је Схакунтала Деви. Али рачунари вам сада омогућавају да целокупну математику учините интелектуалнијом. Концепти и теоре математике су сада више истакнути него икад раније.

Екцел је веома вешт у руковању мноштвом математичких модела, наоружан је огромном колекцијом математичких и логичких функција за подршку различитих операција. Омогућава читав низ тригонометријских функција које нам помажу када кренемо у свет тригонометрије.

Дакле, за решавање тригонометријске функције Сине обезбеђује СИН функцију . То је основна тригонометријска функција, али је корисно посебно ако радите у производњи, навигацији или комуникацијској индустрији. Али важно је напоменути да Екцел користи радијане, а не степене да би израчунао било који тригонометријски израз. Постоје два начина за то:

1. Подсетимо се да је π = 180 °. Дакле, ако је угао у степенима, помножите га са π / 180 ° да бисте га претворили у радијане. У Екцелу се ова конверзија може написати ПИ () / 180. На пример, за претварање 60 ° у радијане, Екцел израз би био 60 * ПИ () / 180 што је једнако 1.0472 радијана.
2. Екцел је такође опремљен врло корисним алатом који се обично назива РАДИАНС. Као аргумент прихвата угао, у којем се угао односи на степене који се морају трансформисати у радијане. Узмимо пример где израз који се користи за претварање 210 ° у радијане је „РАДИАНС (210)“, и процењује на 66519 радијана.

Супротно томе, услужни програм ДЕГРЕЕС је подједнако важан. Ова функција се може користити за супротну функцију РАДИАНС, претварањем радијана у степене. Као пример, ДЕГРЕЕС (ПИ () / 2) оцењује 90.

Како се користи СИН функција у Екцелу?

Разјаснимо како користити СИН функцију у Екцелу помоћу неких примера и стварних илустрација СИН функције у Екцелу.

Овде можете преузети овај СИН Фунцтион Екцел предложак овде - СИН шаблон функције Екцел

СИН функција у Екцелу - пример бр. 1

Израчунавање синусне вредности коришћењем СИН функције у Екцелу

Да бисмо пронашли синус одређеног броја, прво морамо написати = СИН () у одређену ћелију.

Као што видите са горњег снимка заслона, СИН функција у Екцелу очекује број као улаз. Овај број обично представља вредност у радијанима.

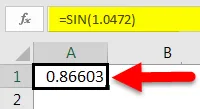
У овом случају ћемо написати „= СИН (1.0472)“, где је 1.0472 радијани еквивалентни 60 степени.

Једном када то учинимо, добићемо вредност СИН од 60 степени.

СИН функција у Екцелу - пример бр. 2

Израчунавање синусне вредности коришћењем СИН и РАДИАН функције у Екцелу

Сада да видимо како можемо СИН користити на продуктивнији начин, у случају када за неки степен не знамо тачну вредност радијана.

Користићемо РАДИАНС () да откријемо радијску вредност, коју ћемо пренети као аргумент СИН функцији.

Дакле, крећемо од старије верзије СИН-а ():

Даље ћемо пренети РАДИАНС (60) као аргумент СИН функцији, где је 60 вредност у степенима.

Као што видимо из горњег примера, РАДИАНС () прихвата вредност у степенима. Дакле, проследићемо 60 као вредност РАДИЈАНИМА ().

Затим притисните Ентер. Ово даје следећи резултат.

Дакле, видимо да је резултат исти као у првом примеру.

СИН функција у Екцелу - пример бр. 3

Израчунавање синусне вредности коришћењем СИН и ПИ функције у Екцелу

Постоји још један начин претварања вредности степена у радијане за нашу употребу у СИН функцији. Сјећамо се из нашег времена у школи да је π = 180 °. Дакле, ако је угао у степенима, помножите га са π / 180 ° да бисте га претворили у радијане. У Екцелу се ова конверзија може написати ПИ () / 180. На пример, за претварање 60 ° у радијане, Екцел израз би био 60 * ПИ () / 180 што је једнако 1.0472 радијана.

Да видимо како то функционише:

Започињемо писањем СИН функције на исти начин као горе.

Затим ћемо директно пренијети 60 ° као аргумент СИН функцији. Али то нам не би дало одговарајућу вредност од 60 степени у радијанима. Стога ћемо помножити 60 са ПИ () / 180.

Ово ће нам дати следећи резултат:

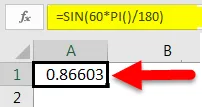
Као што видимо, ово је исто као и горе наведени примери.

СИН функција у Екцелу - пример бр. 4

Погледајмо сада још један пример који приказује резултате СИН функције за различите вредности.

Објашњење резултата приказаних у горњој табели:

Случај 1 и 2:

3.14 је вредност Пи и можемо користити обе методе да бисмо добили вредност 0. То у основи значи да је СИН од Пи радиана 0 .

Случај 3 и 4:

Радианс и Пи / 180 имају једнаку вредност у математици и стога СИН функција даје исту вредност. Оба примера подразумевају СИН од 30 степени што даје вредност 0, 5.

Случај 5 и 6:

СИН 45 = 0, 85 је СИН од 45 радијана што значи да екцел екцел узима све углове у радијанима, а не степен. Да бисмо га претворили у степен можемо користити радијанску функцију и добити СИН од 45 степени као што је приказано у последњем реду. тј. СИН (РАДИЈАНИ (45)) = 0, 707 или 0, 71

СИН функција у Екцелу - Пример 5

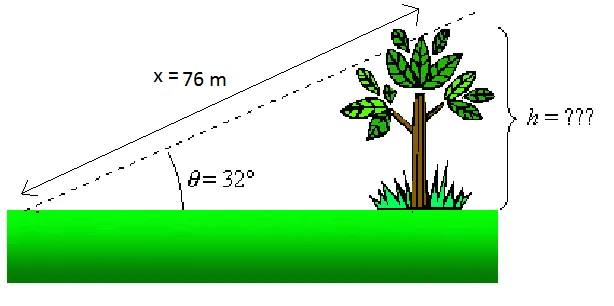
Рецимо, на пример, желимо да знамо висину стабла на слици приказаној горе. Знамо да ако станемо 76 м од врха дрвета (к = 76 м), видна линија према врху стабла је 32 ° у односу на хоризонт (θ = 32 °). Знамо да је:

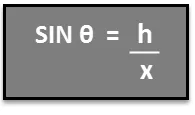
Дакле, да бисмо се решили за висину дрвета х, проналазимо х = к СИН θ.

СИН функција има само један аргумент који је број. За израчун СИН-а потребан је број. Стога је најважније претворити степене у број у радијанима пре него што нађете синус тог нивоа.

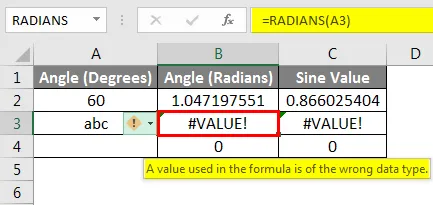
СИН функција приказује # ВАЛУЕ! грешка ако референца која се користи као аргумент функције указује на ћелију која садржи текстуалне податке. У примјеру приказаном у наставку, референца ћелије трећег реда користи се наљепници текста у углу (степени) . Пошто СИН функције подржавају само број као аргумент, СИН ће проценити на грешку, у овом случају # ВАЛУЕ! . Ако ћелија укаже на празну ћелију, функција враћа вредност нула као што је приказано у доњем примеру. Екцел-ове тригонометријске функције тумаче празне ћелије као нулу, а синус нула радијана једнак је нули.

СИН функција у Екцелу - пример бр. 6

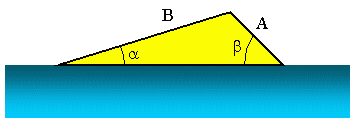
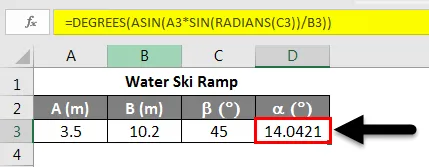
Претпоставимо сада да желимо да откријемо угао покретања рампе за скијање на води као на горњој слици. Знамо да је А = 3, 5 м, Б = 10, 2 м и б = 45, 0 °. Сада, како бисмо пронашли а, можемо користити Закон гријеха. У овом сценарију може се записати као:

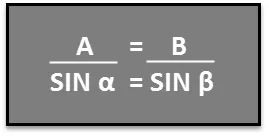
Ову једнаџбу можемо поново организовати као:

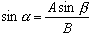
Помоћу лучног или инверзног синуса можемо сазнати угао α . Примена једначине приказане доле.

Пример бр. 7

У нашем коначном тригонометријском примеру користићемо Екцел за испитивање тригонометријског идентитета:

син²θ + цос²θ = 1

Имајте на уму да на слици испод овај идентитет важи када је θ дат у радијанима и у степенима.

Имајте на уму да је опис јединице за угао θ смештен у различите ћелије од бројева. Ако бројеве и јединице ставимо у исту ћелију, Екцел неће моћи да разликује број од текста и зато нећемо моћи да референцирамо ћелије за употребу у једначини и то ће резултирати # ВАЛУЕ! грешка.

Ствари које треба запамтити

• Имајте на уму да СИН функција у екцелу подразумевано ради са Радианом.
• Претворите број према захтеву у Радиан или Степен користећи било РАДИАНС или ДЕГРЕЕС функцију.
• Можете користити функцију ПИ () да бисте добили тачне резултате СИН функције током рада са π.

Препоручени чланци

Ово је водич за СИН функцију у Екцелу. Овде смо разговарали о томе како се користи СИН функција у Екцелу заједно са практичним примерима и довнлоад-ом Екцел предлошка. Можете и да прођете кроз друге наше предложене чланке -

1. Важне функције математике у Екцелу (лако)
2. Водич за поделу формуле у Екцелу
3. Важне напредне формула и функције Екцел-а
4. Схеет оф Екцел Формулас