
Увод у функције у Р
Функција је дефинисана као скуп исказа, да изврши и изврши било који одређени логички задатак. Функција узима неке улазне параметре који су познати као аргументи за извршавање тог задатка. Функције помажу у разбијању кода, на једноставније делове логичким оркестрирањем, што је лакше за читање и разумевање. У овој теми сазнаћемо о Функцијама у Р.
Како написати функције у Р?
Да бисте функцију написали у Р, ево синтаксе:
Fun_name <- function (argument) (
Function body
)
Овде се може видети „функција“ специфична резервисана реч која се користи у Р за дефинисање било које функције. Функција узима улаз који је у облику аргумената. Тело функције је скуп логичких изјава које се изводе преко аргумената и тада враћа излаз. „Фун_наме“ је име датој функцији, преко које се може позвати било где у Р програму.
Погледајмо пример, који ће бити луциднији у разумевању концепта функције у Р.
Р код
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
излаз:
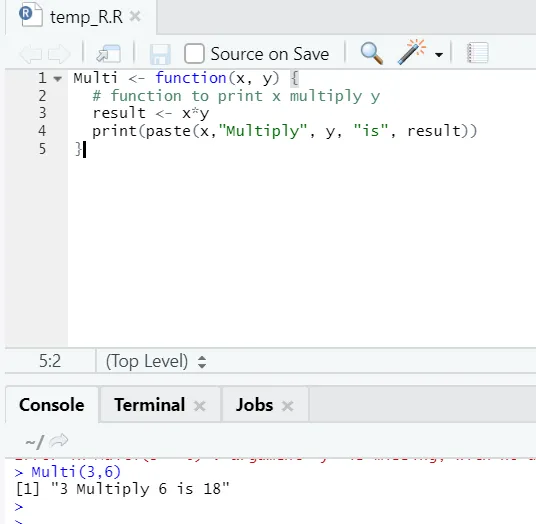
Овде смо створили назив функције „Мулти“, који узима два аргумента као улаза и пружа мултипликован излаз. Први аргумент је к, а други аргумент и. Као што видите, функцију смо назвали именом "Мулти". Овде ако неко жели, аргументи се такође могу поставити на задану вредност.
Различите врсте функција у Р
Различите Р функције са синтаксом и примерима (уграђени, математички, статистички итд.)
1) Уграђена функција -
Ово су функције које долазе са Р за решавање одређеног задатка узимајући аргумент као улаз и дајући излаз на основу датог уноса. Овде ћемо разговарати о неким важним општим функцијама Р:
а) Сортирање: Подаци могу бити сортирани по узлазном или силазном редоследу. Подаци могу бити да ли је вектор континуиране варијабле или факторска варијабла.
Синтакса:

Ево објашњења његових параметара:
- к: Ово је вектор непрекидне променљиве или факторске променљиве
- опадајући: Ово се може поставити или Труе / Фалсе да би контролисао редослед узлазним или силазним редоследом. Подразумевано је ФАЛСЕ`.
- задњи: Ако вектор има НА вредности, треба ли га ставити задњи или не
Р код и излаз:
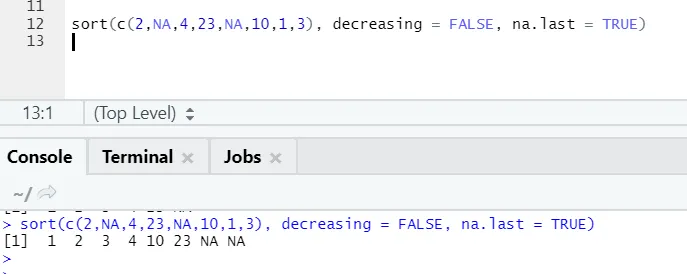
Овде се може приметити како се „НА“ вредности поравнавају на крају. Како је био наш параметар на.ласт = Труе.
б) Сек: Ствара редослед броја између два наведена броја.
Синтакса
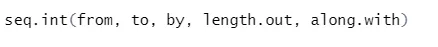
Ево објашњења његових параметара:
- од, за почетну и крајњу вредност низа.
- по: Повећање / размак између два узастопна броја у низу
- ленгтх.оут: потребна дужина секвенце.
- Дуж.витх: Односи се на дужину од дужине овог аргумента
Р код и излаз:
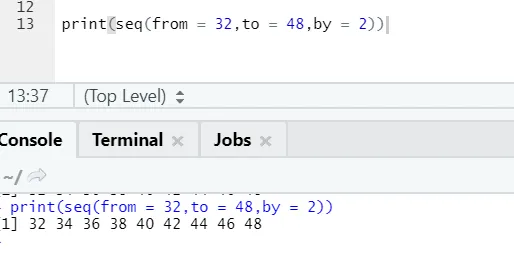
Овде се може приметити да настали низ има инкременцију 2, јер је дефинисан као 2.
ц) Тоуппер, толовер: Две функције: тоуппер и толовер су функције које се примењују на низу за промену почетних слова слова у реченицама.
Р код и излаз:
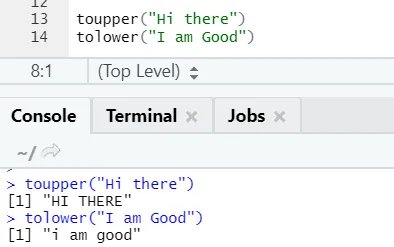
Може се приметити како се случајеви слова мијењају када се примијене на функцију.
д) Рнорм: Ово је уграђена функција која генерише случајне бројеве.
Р код и излаз:
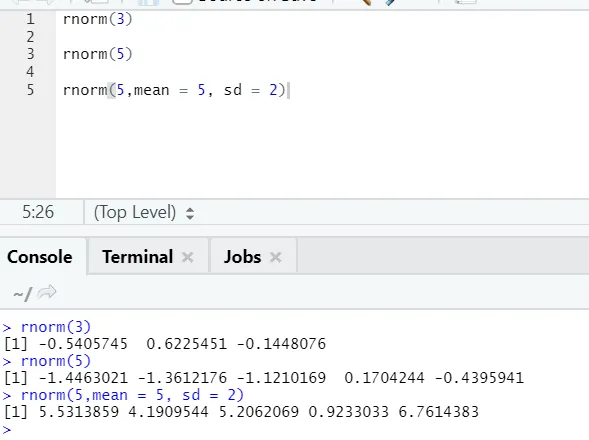
Функција рнорм узима први аргумент који каже колико бројева треба генерисати.
е) Реп: Ова функција понавља вриједност онолико пута колико је специфицирано.
Р синтакса: рнорм (к, н)
Овде к представља вредност за реплицирање, а н представља број колико треба поновити.
Р код и излаз:
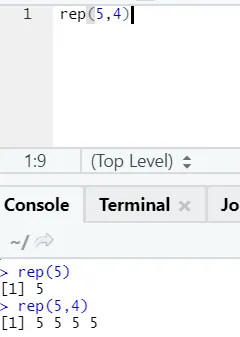
ф) Налепи: Ова функција је спајање низова заједно са неким специфичним карактером између.
синтакса
paste(x, sep = “”, collapse = NULL)
Р код
paste("fish", "water", sep=" - ")
Р излаз:
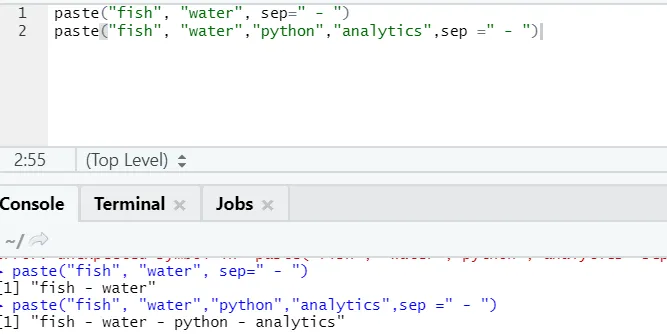
Као што видите, можемо да залепимо и више од две жице. Сеп је онај специфичан лик који смо додали између жице. Сеп је подразумевано простор.
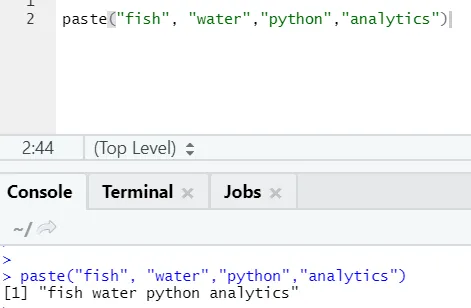
Постоји још једна слична функција ове, коју би сви требали бити свесни, је пасте0.
Функција пасте0 (к, и, колапс) делује слично као пасте (к, и, сеп = "", колапс)
Молимо погледајте пример испод:
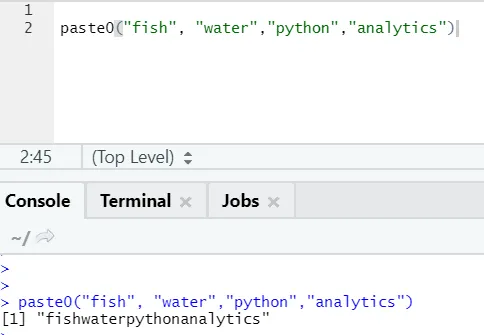
Једноставним речима, да сумирамо пасте и пасте0:
Пасте0 је бржи од пасте када је у питању спајање низова без раздвајања. Пошто пасте увек траже „сеп“ и који је у њему подразумевани простор.
г) Стрсплит: Ова функција је за поделу низа. Погледајмо једноставне случајеве:
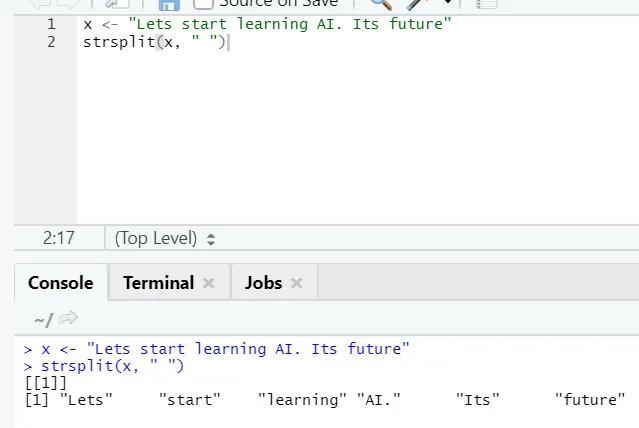
х) Рбинд: функција рбинд помаже у чешању вектора са истим бројем ступаца, један преко другог.
Пример
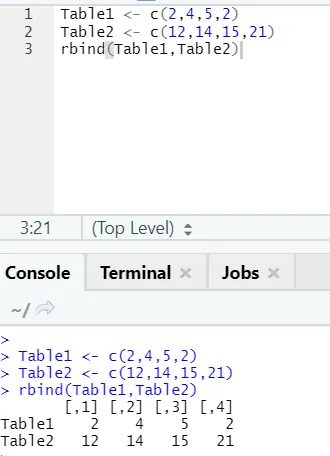
и) цбинд: Ово комбинује векторе са истим бројем редова, један поред другог.
Пример
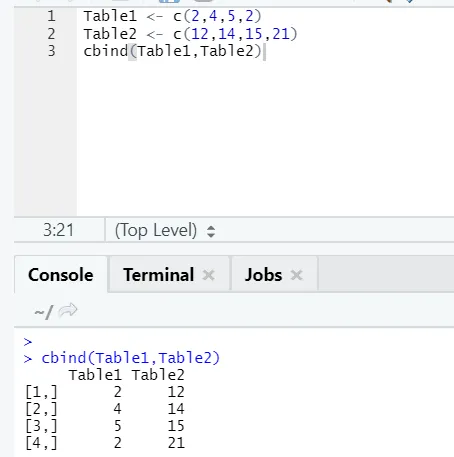
У случају да се број редова не подудара, испод је грешка коју ћете наћи:

И цбинд и рбинд помажу у манипулацији и преобликовању података.
2) Матх функција -
Р пружа широк избор математичких функција. Погледајмо неколико њих детаљно:
а) Скрт: Ова функција израчунава квадратни корен броја или нумеричког вектора.
Р код и излаз:
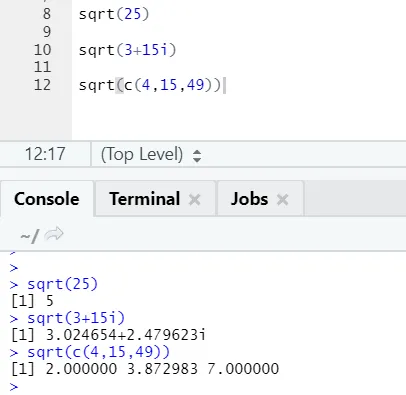
Може се видети како се израчунава корен броја, сложеног броја и низа нумеричких вектора.
б) Екп: Ова функција израчунава експоненцијалну вредност броја или нумеричког вектора.
Р код и излаз:
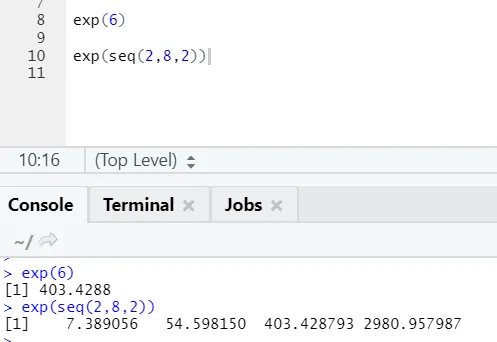
ц) Цос, Син, Тан: Ово су функције тригонометрије имплементиране у Р овде.
Р код и излаз:
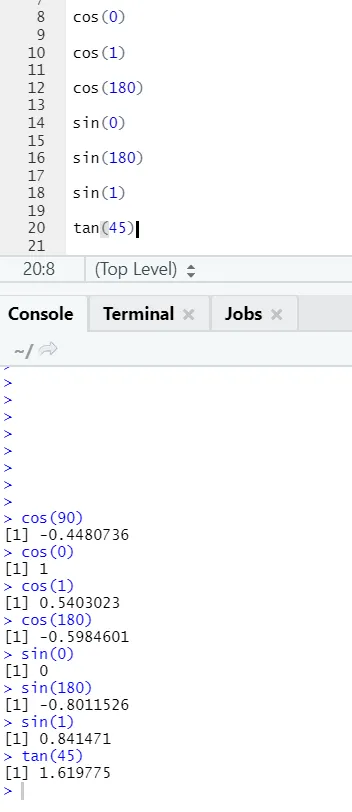
д) Абс: Ова функција враћа апсолутну позитивну вредност броја.
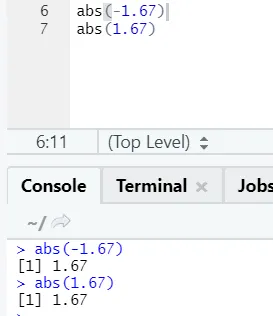
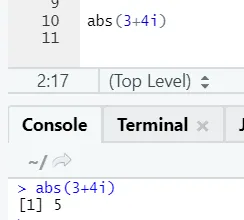
Као што видите, негативни или позитивни бројеви ће се вратити у свом апсолутном облику. Погледајмо га за сложен број:
е) Дневник: Ово је проналазак логаритма броја.
Ево примера који је приказан у наставку:
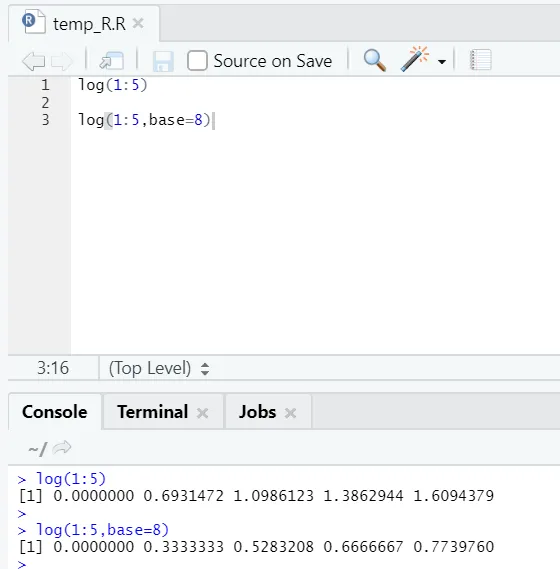
Овде се добија флексибилност за промену базе, према захтевима.
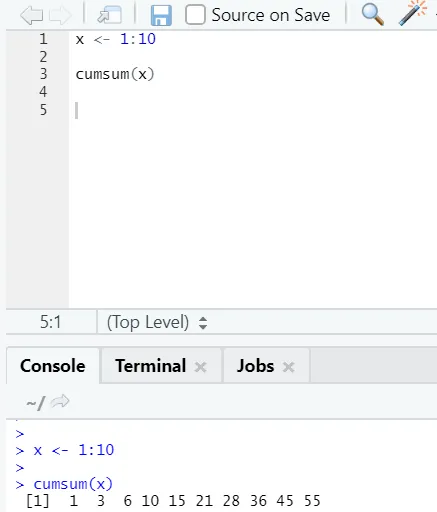
ф) Цумсум: Ово је математичка функција која даје кумулативне суме. Ево следећег примера:
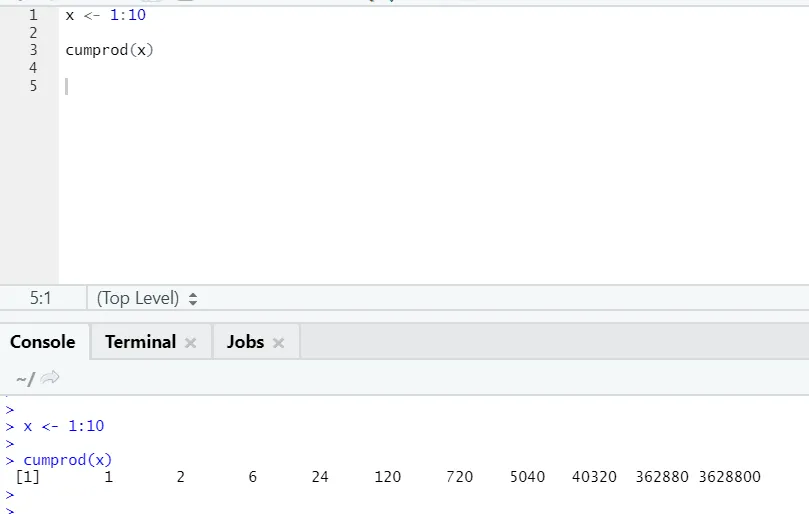
г) Цумпрод: Као и Цумсумова математичка функција, имамо и цумпрод тамо где се догађа кумулативно множење.
Молимо погледајте пример испод:
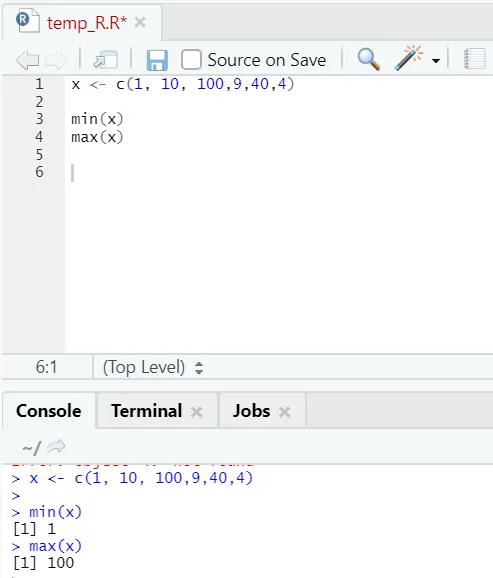
х) Мак, Мин: Ово ће вам помоћи да пронађете максималну / минималну вредност у скупу бројева. Погледајте доле примере везане за ово:
и) Плафон: Плафон је математичка функција враћа најмањи од целог броја већи од наведеног.
Погледајмо пример:
плафон (2.67)
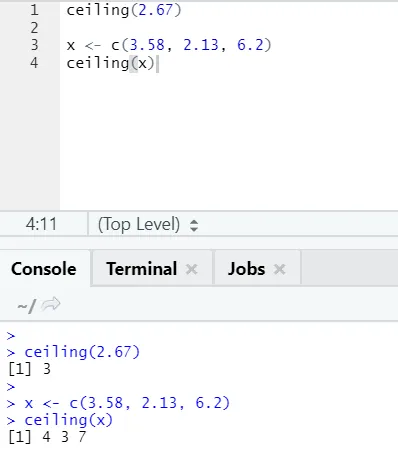
Као што можете приметити, таваница се примењује преко броја, као и преко неке листе, а излазни резултат је најмањи од следећег већег целог броја.
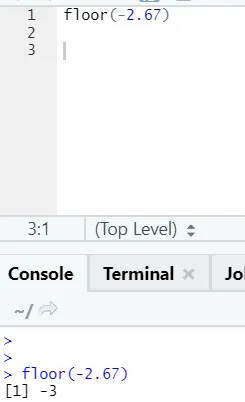
ј) Спрат: Под је математичка функција враћа најмању вриједност цијелог броја од наведеног броја.
Пример приказан у наставку помоћи ће вам да боље разумете:
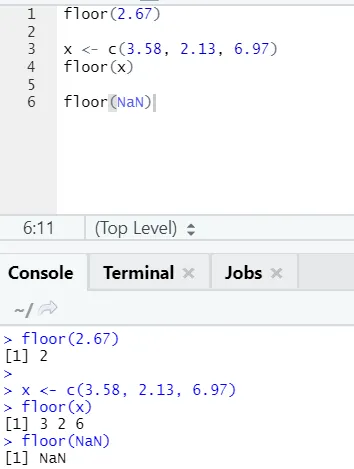
Исто функционише и за негативне вредности. Молимо вас да погледате:
3) Статистичке функције -
Ово су функције које описују повезану дистрибуцију вероватноће.
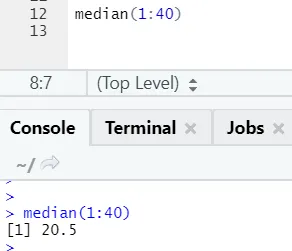
а) Медијана: Ова средња вредност се израчунава из низа бројева.
Синтакса
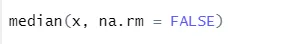
Р код и излаз:
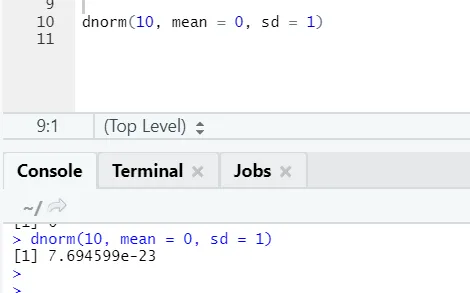
б) днорма: односи се на нормалну дистрибуцију. Функција днорм враћа вриједност функције густоће вјероватноће, за нормалну расподјелу даних параметара за к, μ и σ.
Р код и излаз:
ц) Цов: Коваријанција говори да ли су два вектора позитивно, негативно или потпуно повезана.
Р код
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
Р излаз:
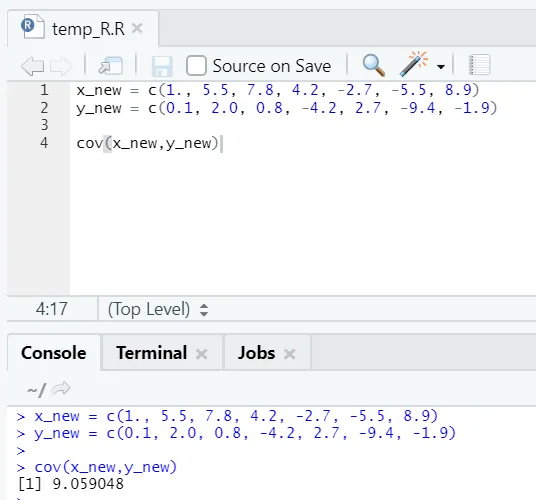
Као што видите, два вектора су позитивно повезана, што значи да се оба вектора крећу у истом правцу. Ако је коваријанс негативан, то значи да су к и и обрнуто повезани и стога се креће у супротном смеру.
д) Цор: Ово је функција за проналажење корелације између вектора. Заправо даје фактор асоцијације између два вектора који је познат и као „коефицијент корелације“. Корелација додаје фактор степена у односу на коваријанс. Ако су два вектора позитивно повезана, корелација ће вам такође рећи колико су они позитивно повезани.
Ове три врсте метода које се могу користити за проналажење корелације између два вектора:
- Пеарсонова корелација
- Кендалл корелација
- Корелација Спеармана
У једноставном Р формату изгледа:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Овде су к и и вектори.
Погледајмо практични пример корелације преко уграђеног скупа података.
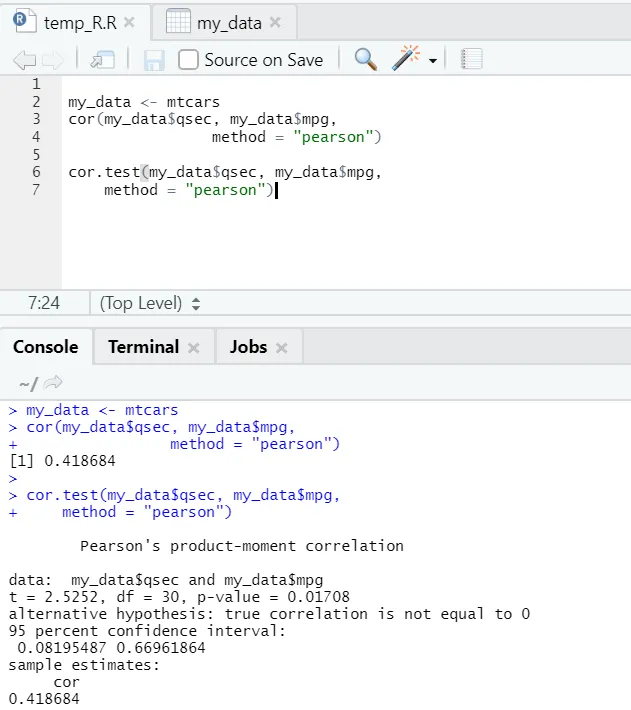
Дакле, овде можете видети да је функција "цор ()" дала коефицијент корелације 0, 41 између "ксец" и "мпг". Међутим, приказана је још једна функција, тј. "Цор.тест ()", која не само да говори коефицијент корелације, већ и п-вредност и т вредност која је с њим повезана. Интерпретација постаје далеко лакша помоћу функције Цор.тест.
Слично се може урадити и са друга два начина корелације:
Р код Пеарсонове методе:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
Р код Кендалл методе:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
Р код за Спеарман метод:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
Коефицијент корелације се креће између -1 и 1.
Ако је коефицијент корелације негативан, то значи када се к повећава и смањује.
Ако је коефицијент корелације једнак нули, то значи да не постоји повезаност између к и и.
Ако је коефицијент корелације позитиван, то подразумева када се к повећава и такође има тенденцију повећања.
е) Т-тест: Т-тест ће вам рећи да ли два скупа података потичу из исте (под претпоставком) нормалне дистрибуције или не.
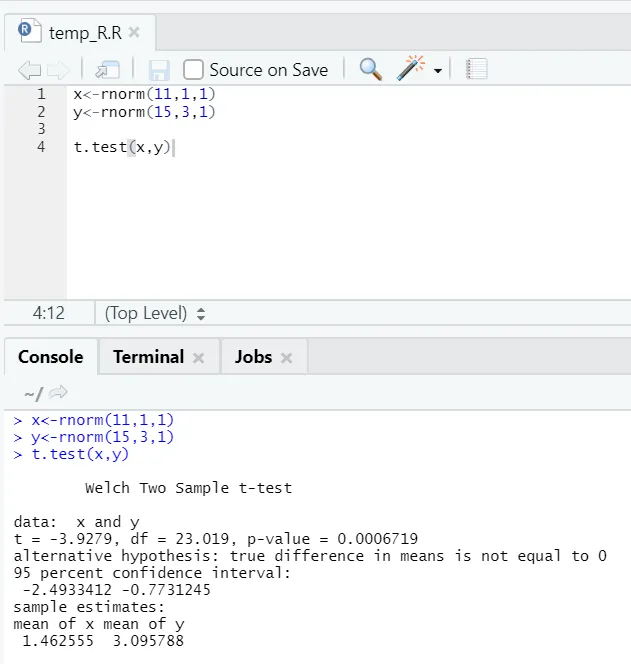
Овде бисте требали одбацити нулту хипотезу да су два средства једнака јер је п-вредност мања од 0, 05.
Ова приказана инстанца је типа: непарни скупови података са неједнаким одступањима. Слично томе, може се покушати и са упареним подацима.
ф) Једноставна линеарна регресија: Ово показује однос између предиктора / независне и променљиве која зависи од одговора.
Једноставним практичним примером могло би се предвидети тежину особе ако се зна висина.
Р синтакса
lm(formula, data)
Овде формула приказује однос између излаза тј. И и улазне променљиве иек Подаци представљају скуп података на који се формула мора применити.
Погледајмо један практичан пример, где је површина пода улазна променљива, а закуп је излазна променљива.
к <- ц (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
и <- ц (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
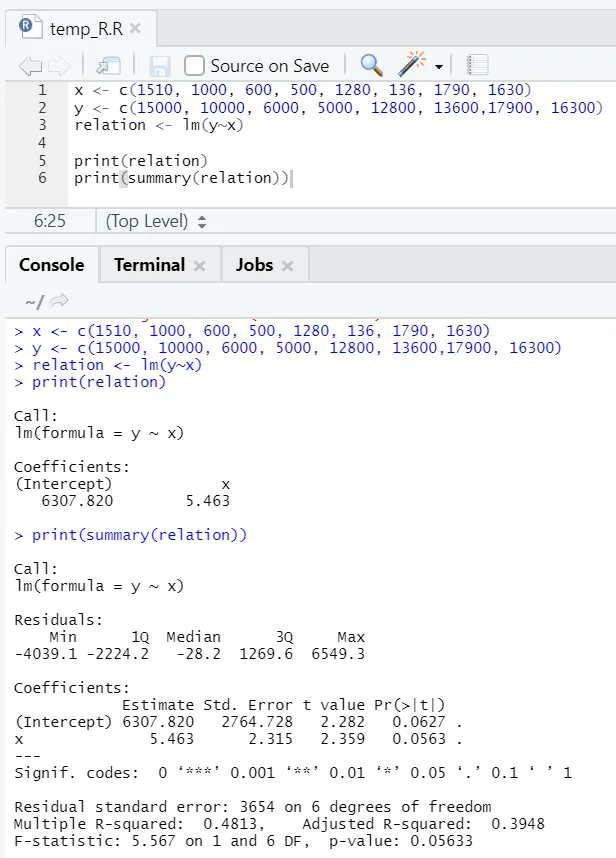
Овде П-вредност није мања од 5%. Отуда ниједна хипотеза не може бити одбачена. Нема много значаја за доказивање односа између површине пода и станарине.
Овде је вредност Р-квадрата 0, 4813. То подразумева само 48% варијанце излазне променљиве може се објаснити улазном променљивом.
Рецимо сада да требамо предвидјети вриједност површине пода, на основу горе постављеног модела.
Р код
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
Р излаз:
Након извршења горњег Р кода, излаз ће изгледати следеће:
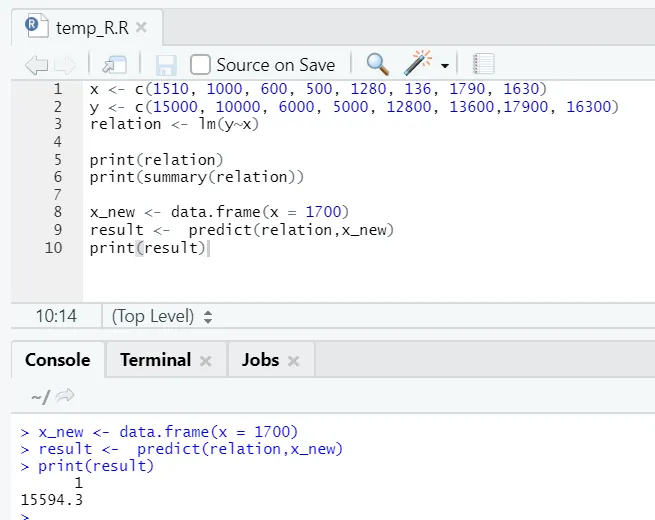
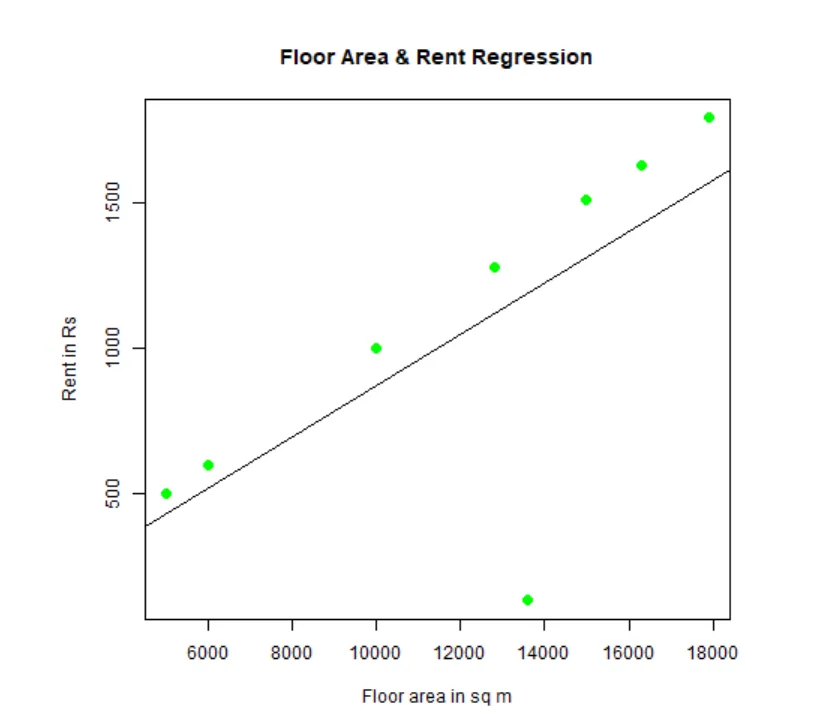
Може се уклопити и визуелизовати регресија. Ево Р кода за то:
# Дајте име датотеци пнг графикона.
png(file = "LinearRegressionSample.png.webp")
# Нацртајте графикон.
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Сачувај датотеку.
dev.off()
Овај графикон „ЛинеарРегрессионСампле.пнг“ биће генерисан у вашем тренутном радном директорију.
г) тест Цхи-Скуаре
Ово је статистичка функција у Р. Овај тест има свој значај да би доказао да ли постоји повезаност између две категоријске променљиве.
Овај тест такође делује као и било који други статистички тестови који су се заснивали на п-вредности, може се прихватити или одбацити нулта хипотеза.
Р синтакса
chisq.test(data), /code>
Погледајмо један практични пример тога.
Р код
# Учитајте библиотеку.
library(datasets)
data(iris)
# Креирајте оквир података из главног скупа података.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Направите табелу са потребним променљивим.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Извршите тест Цхи-Скуаре.
print(chisq.test(iris.data))
Р излаз:
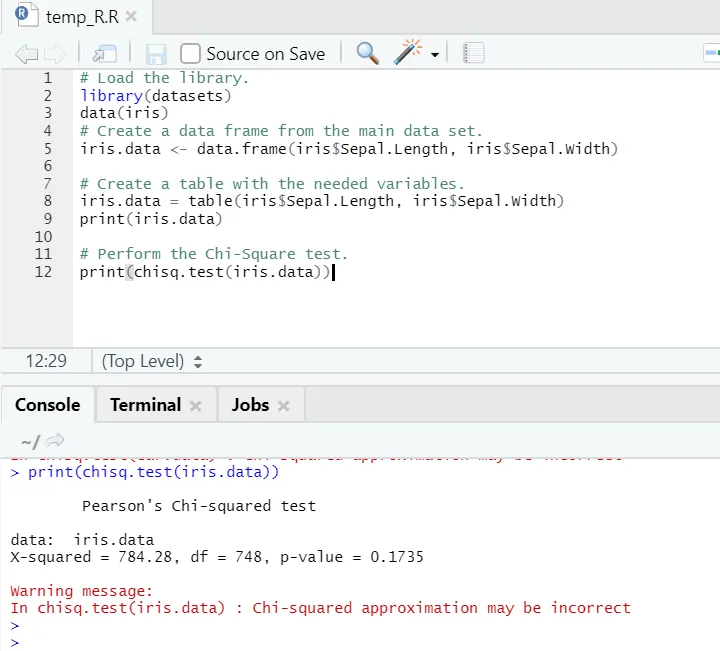
Као што се може видети, тест хи-квадрата изведен је на бази ириса, с обзиром на његове две променљиве „Сепал. Дужина “и„ Сепал.Видтх “.
П-вредност није мања од 0, 05, те стога не постоји корелација између ове две променљиве. Или можемо рећи да ове две променљиве не зависе једна од друге.
Закључак
Функције у Р су једноставне, лако се постављају, лако се разумеју и веома су моћне. Видели смо разне функције које се као део основа користе у Р. Када се неко угоди овим функцијама које смо горе размотрили, можемо истражити и друге врсте функција. Функције вам помажу, а код се покреће на једноставан и сажет начин. Функције могу бити уграђене или кориснички дефинисане, све зависи од потребе док се бавите проблемом. Функције дају доброј форми програму.
Препоручени чланци
Ово је водич за Функције у Р., овде смо расправљали о начину писања функција у Р и различитих врста функција у Р синтакси и примерима. Такође можете погледати следећи чланак да бисте сазнали више -
- Р стринг функције
- СКЛ стринг функције
- Функције стрингова Т-СКЛ
- ПостгреСКЛ стринг стринг функције