
Формула Ф-теста (Садржај)
- Формула
- Примери
Шта је Ф-тест формула?
Ф-тест је статистички тест који нам помаже да утврдимо да ли два скупа популације који имају нормалну расподјелу својих података имају исту стандардну девијацију или варијанцу. Али прво и најважније за обављање Ф-теста је да скупови података треба да имају нормалну дистрибуцију. Ово се примењује на Ф дистрибуцију под нултом хипотезом. Ф-тест је веома важан део анализе варијанце (АНОВА) и израчунава се узимањем односа две варијације два различита скупа података. Као што знамо да нам одступања дају информације о раширености тачака података. Ф-тест се такође користи у разним тестовима попут регресијске анализе, Цхов теста итд.
Формула за Ф-тест:
Не постоји једноставна формула за Ф-тест, али то је низ корака које морамо следити:
Корак 1: Да бисмо извели Ф-тест, прво морамо дефинисати нулту хипотезу и алтернативну хипотезу. Они су добили од:
- Х0 (Нулл Хипотхесис): Варијација 1. скупа података = Варијанта другог скупа података
- Ха: Варијанта првог скупа података <Варијанта другог скупа података (за доњи тест са једним репом)
- Ха: Варијанта првог скупа података> Варијанта другог скупа података (за горњи тест с једним репом)
- Ха: Варијанта првог скупа података = Варијанта другог скупа података (за дворедни тест)
Корак 2: Следеће што морамо учинити је да пронађемо ниво значаја и затим одредимо степене слободе и бројача и називника. То нам помаже у одређивању њихових критичних вредности. Степен слободе је узорак величине -1.
Корак 3: Формула Ф-теста:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
Корак 4: Пронађите Ф критичну вредност из Ф табеле, узимајући степен слободе и нивоа значаја.
Корак 5: Упоредите ове две вредности и ако је критична вредност мања од Ф вредности, можете одбацити нулту хипотезу.
Примери формуле Ф-теста (са Екцеловим предлошком)
Узмимо пример како бисмо боље разумели израчунавање Ф-теста.
Можете преузети овај Ф-ТЕСТ образац за Екцел формулу овде - Ф-ТЕСТ Формула Екцел предложакФормула Ф-теста - пример бр. 1
Рецимо да имамо два скупа података А&Б који садрже различите тачке података. Извршите Ф-тест како бисмо утврдили да ли можемо одбацити нулту хипотезу на нивоу важности од 1%.
Скупови података:
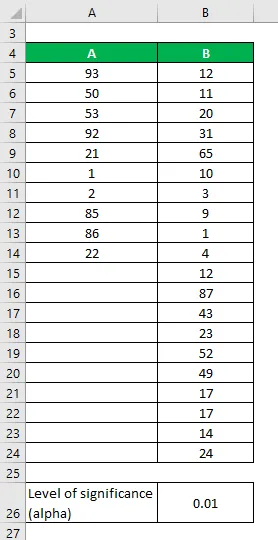
Решење:
Нулта хипотеза: Варијација А = Варијанта Б
Степен слободе се израчунава као
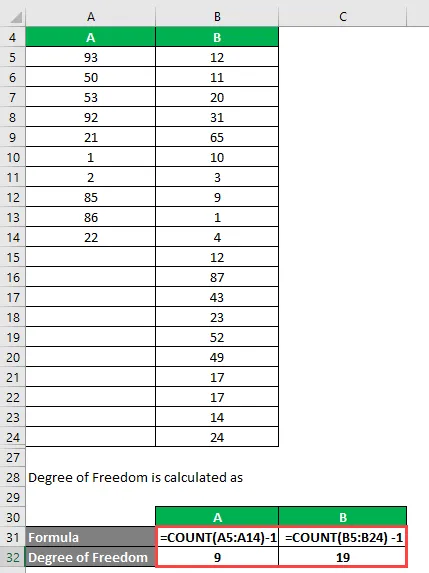
Степен слободе
- За А = 10 - 1 = 9
- За Б = 20 - 1 = 19
Варијација се израчунава као:

- Варијација А = 1385, 61
- Варијанта Б = 521.22
Вредност се израчунава према нижој формули
Ф Вредност = Варијација 1. скупа података / Варијанта другог скупа података
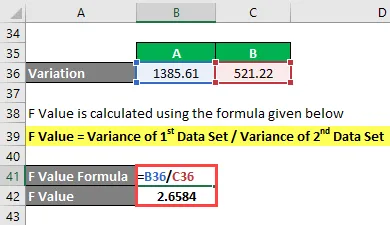
- Ф Вредност = 1385.61 / 521.22
- Ф Вредност = 2.6584
Ф-табела:
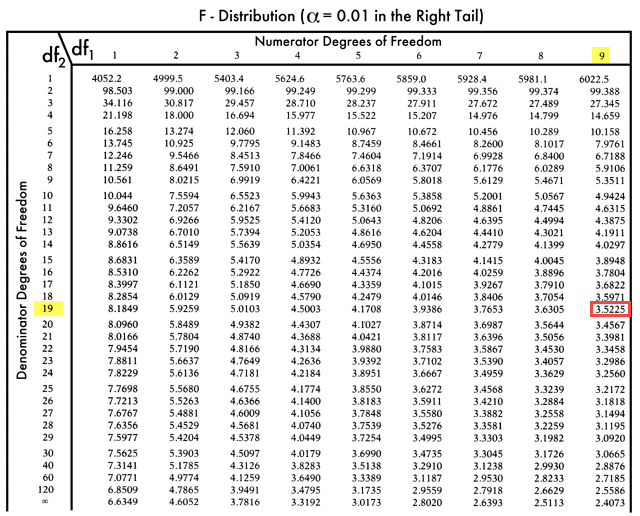
Дакле, Ф критична вредност = 3, 5225
Пошто је Ф критична већа од Ф вредности, не можемо одбацити ништавну хипотезу.
Формула Ф-теста - пример бр. 2
Претпоставимо да радите у истраживачкој компанији и желите да ниво емисије угљен-оксида који се догађа од две различите марке цигарета и да ли су оне значајно различите или не. У својој анализи сте прикупили следеће информације:
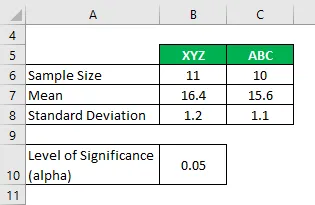
Решење:
Степен слободе се израчунава као
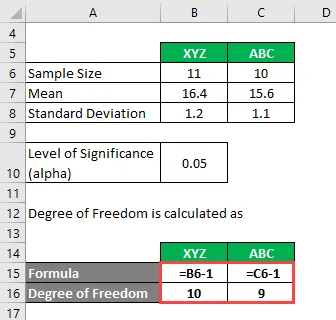
Степен слободе
- За КСИЗ = 11 - 1 = 10
- За АБЦ = 10 - 1 = 9
Варијација се израчунава као:
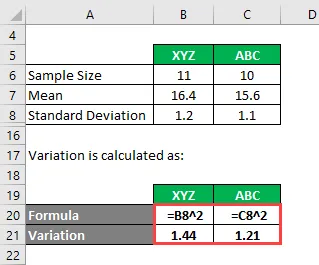
- Варијанта КСИЗ = 1, 2 2 = 1, 44
- Варијанта АБЦ = 1.1 2 = 1.21
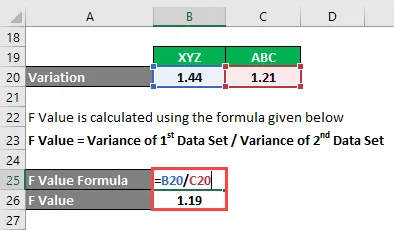
- Ф Вредност = 1, 44 / 1, 21
- Ф вредност = 1, 19
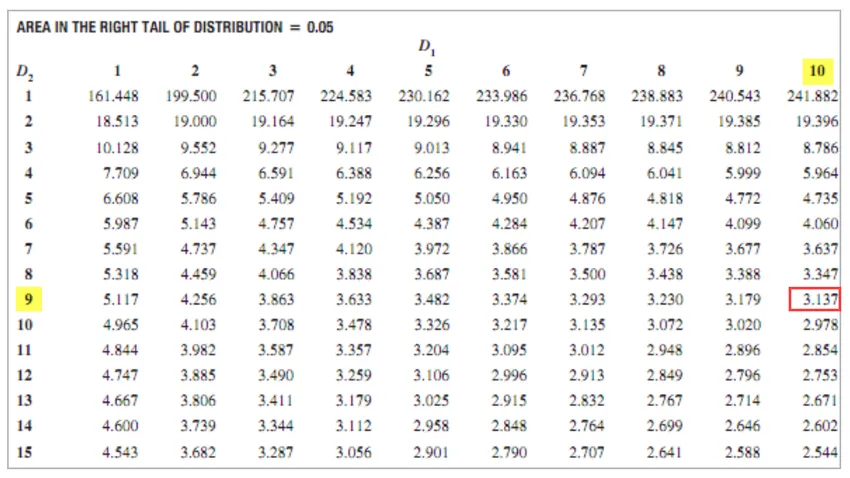
Ф критична вредност = 3.137
Пошто је вредност Ф критична> Ф, нулта хипотеза се не може одбити.
Објашњење
У горњим примерима видели смо примену Ф-теста и како се изводи. Али постоји скуп претпоставки на које морамо водити рачуна пре него што извршимо Ф-тест у супротном нећемо добити тражене резултате:
- Прво је да увек требамо постављати већи бројник одступања током израчунавања Ф вредности. Дакле, ако је Ф = В1 / В2, В1 би требао бити> В2
- Ако желимо да извршимо 2 репа испитивања, морамо да поделимо ниво значајности на 2 и то ће бити тачан ниво да бисмо пронашли критичну вредност
- Користимо само варијанцу је израчунавање вредности Ф и ако нам се дају са стандардним одступањима, као у примеру 2, они морају бити уврштени у квадрат да би пронашли варијанцу.
- Оба узорка треба да буду независна један од другог, а величина узорка треба да буде мања од 30
- Скупине популације из којих се узимају узорци морају се нормално расподијелити
Ово су кључни параметри / претпоставке на које треба водити рачуна приликом извођења Ф-теста.
Релевантност и употреба формуле Ф-теста
Ф-тест, као што је горе дискутирано, помаже нам да проверимо једнакост две варијације популације. Дакле, када имамо два независна узорка која су узета из нормалне популације и желимо да проверимо да ли имају исту варијабилност или не, користимо Ф-тест. Ф-тест такође има велику важност у регресијској анализи и такође за тестирање значаја Р2. Укратко, Ф-Тест је веома важан алат у статистици ако желимо да упоредимо варијације два или више скупова података. Али треба имати на уму све претпоставке пре обављања овог теста.
Препоручени чланци
Ово је водич за Ф-тест формуле. Овде смо расправљали о томе како израчунати Ф-тест заједно са практичним примерима и довнлоад-ом Екцел шаблона. Такође можете погледати следеће чланке да бисте сазнали више -
- Т Формула дистрибуције
- Формула за цене обвезница
- Формула процента грешке
- Прорачун формуле НОПАТ