Линеарна регресија у Екцелу - Како урадити линеарну регресију у Екцелу?

Линеарна регресија у Екцелу (Садржај)

Увод у линеарну регресију у Екцелу
Методе за употребу линеарне регресије у Екцелу

Увод у линеарну регресију у Екцелу

Линеарна регресија је статистичка техника / метода која се користи за проучавање односа две континуиране квантитативне променљиве. У овој техници, независне променљиве се користе за предвиђање вредности зависне променљиве. Ако постоји само једна независна варијабла, онда је то једноставна линеарна регресија, а ако је број независних променљивих више од једне, онда је то вишеструка линеарна регресија. Модели линеарне регресије имају однос између зависних и независних варијабли постављањем линеарне једначине на посматране податке. Линеарно се односи на чињеницу да користимо линију како би одговарала нашим подацима. Зависне променљиве које се користе у регресијској анализи такође се називају реактивне или предвиђене променљиве, а независне променљиве се такође називају објасњавајућим променљивим или предикторима.

Линеарна регресијска линија има једначину врсте: И = а + бКс;

Где:

Кс је објасњавајућа променљива,
И је зависна варијабла,
б је нагиб линије,
а је пресретање и (тј. вредност и када је к = 0).

Метода најмање квадрата се опћенито користи у линеарној регресији која израчунава најприкладнију линију за проматране податке минимизирајући збир квадрата одступања података са линије.

Методе за употребу линеарне регресије у Екцелу

Овај пример вас учи методама за обављање линеарне регресијске анализе у Екцелу. Погледајмо неколико метода.

Овде можете преузети овај Линеар Регрессион Екцел предложак овде - Линеар Регрессион Екцел предложак

Метода бр. 1 - скаттер са тренд-линијом

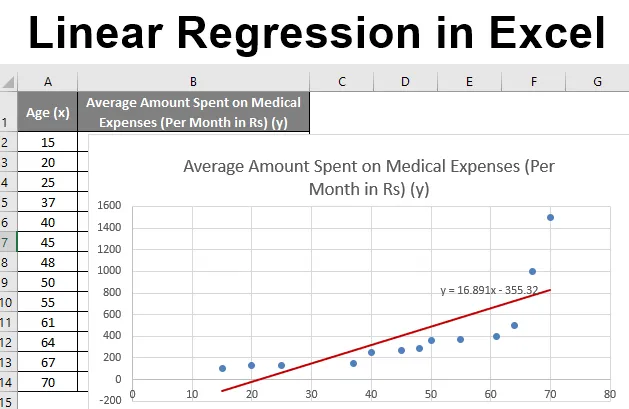
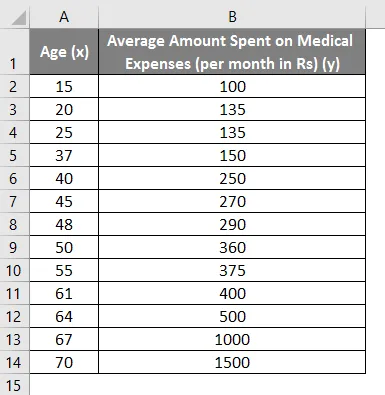
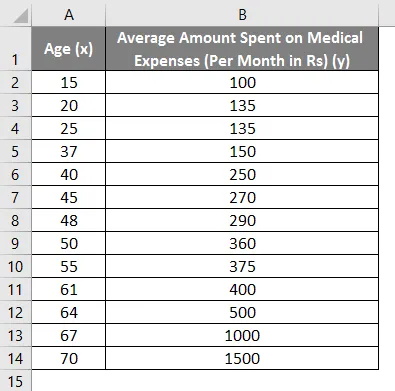
Рецимо да имамо скуп података о појединцима с њиховом старошћу, индексом биомасне масе (БМИ) и количином коју су потрошили на медицинске трошкове у току једног месеца. Сада, са увидом у особине појединаца као што су старост и БМИ, желимо да пронађемо како ове променљиве утичу на трошкове лечења, па их користимо за спровођење регресије и процену / предвиђање просечних трошкова за неке поједине особе. Погледајмо прво како само старост утиче на трошкове лечења. Погледајмо скуп података:

Износ за медицинске трошкове = б * старост + а

Изаберите два ступца скупа података (к и и), укључујући заглавља.

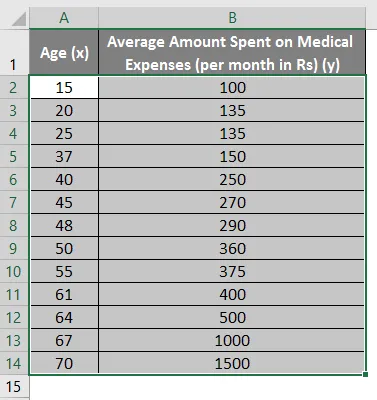
Кликните на 'Инсерт' и проширите падајући мени за 'Сцаттер Цхарт' и одаберите сличицу 'Сцаттер' (прва)

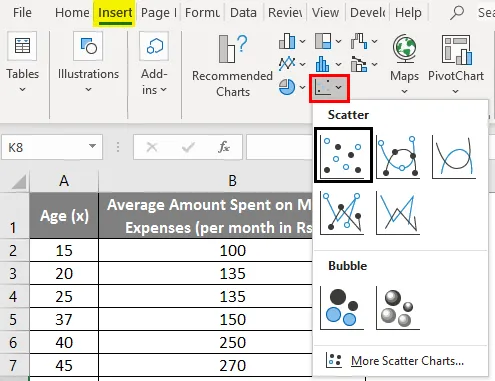
Сада ће се појавити заплет распршивања и на томе бисмо нацртали регресијску линију. Да бисте то учинили, кликните десним тастером миша на било коју тачку података и изаберите „Додај тренд линију“

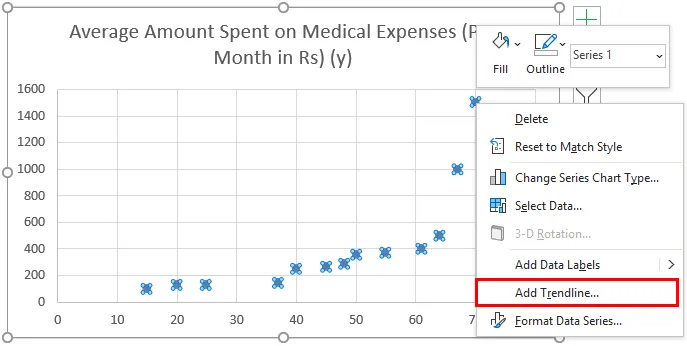
Сада у окну 'Обликуј трендовску линију' десно, изабери 'Линеар Трендлине' и 'Дисплаи Екуатион он Цхарт'.

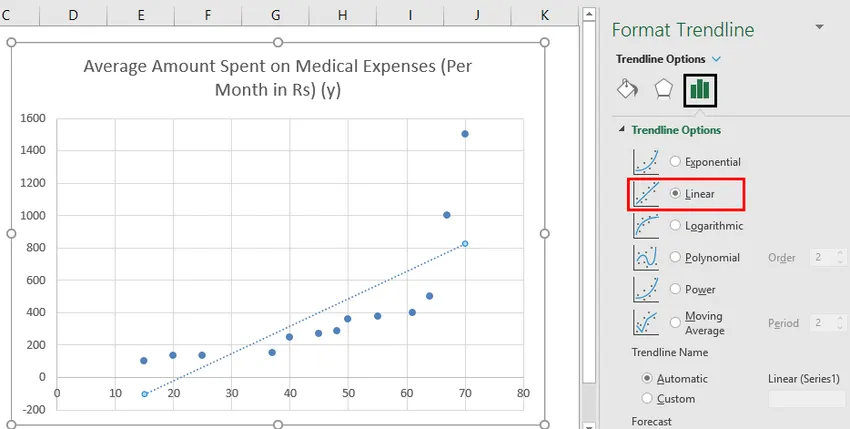
Изаберите „Прикажи једнаџбу на графикону“.

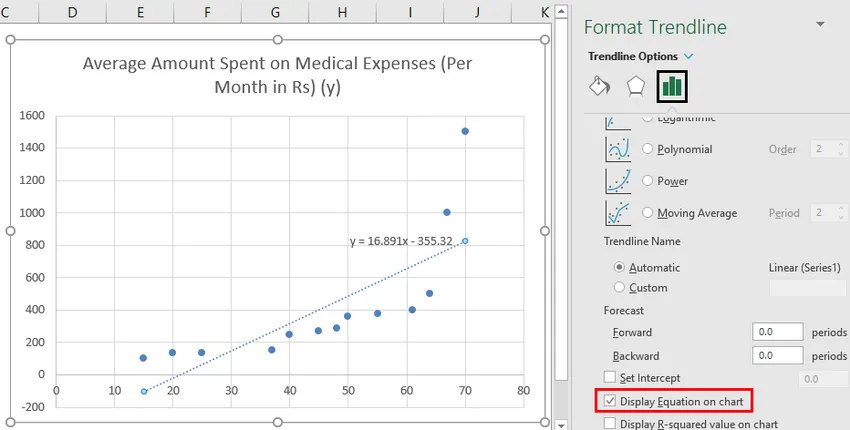
Можемо импровизовати графикон према нашим захтевима, попут додавања наслова оси, промене скале, боје и врсте линија.

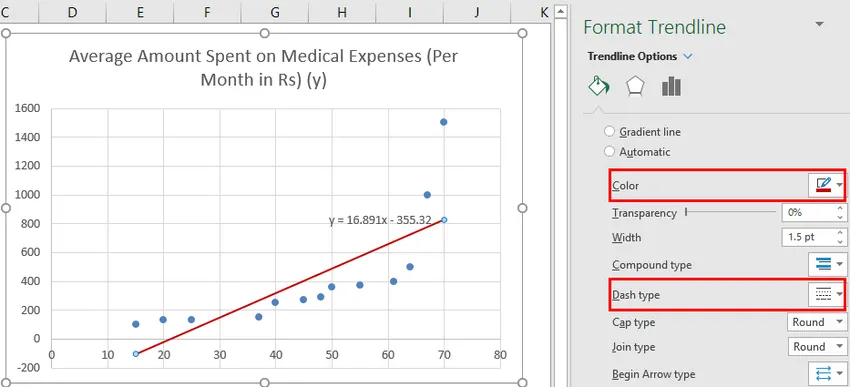
Након импровизације графикона ово је резултат који добијамо.

Напомена: У овом типу регресијског графикона, зависна променљива увек треба да буде на оси и, а независна на к-оси. Ако се графикон црта обрнутим редоследом, или пребаците осе у графикон, или замените ступце у скупу података.

Метода бр. 2 - Метода додавања за ТоолПак за анализу

Аналисис ТоолПак понекад није омогућен подразумевано и то морамо да урадимо ручно. Урадити тако:

Кликните на мени „Датотека“.

Након тога кликните на 'Опције'.

Изаберите „Додаци за Екцел“ у пољу „Управљање“ и кликните на „Иди“

Изаберите „Аналисис ТоолПак“ -> „ОК“

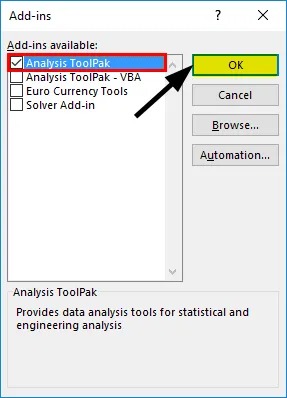
Ово ће додати алате „Анализа података“ на картицу „Подаци“. Сада покрећемо регресијску анализу:

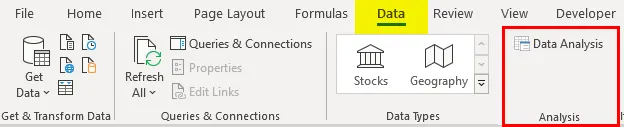
Кликните на 'Анализа података' на картици 'Подаци'

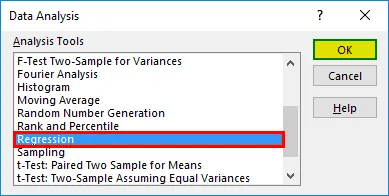
Изаберите „Регресија“ -> „ОК“

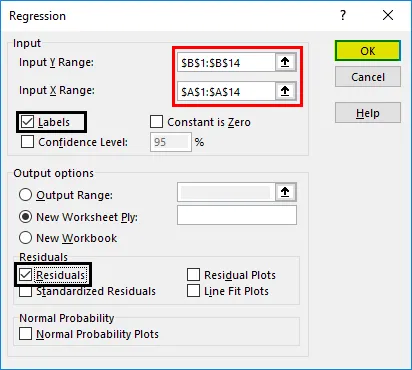
Појавиће се дијалошки оквир за регресију. Изаберите опсег уноса И и распон улаза Кс (медицински трошкови и старост, респективно). У случају вишеструке линеарне регресије, можемо одабрати више ступаца независних променљивих (нпр. Ако желимо да видимо утицај БМИ као и на медицинске трошкове).
Потврдите поље „Етикете“ да бисте укључили заглавља.
Изаберите жељену опцију 'оутпут'.
Потврдите потврдни оквир 'заостаци' и кликните на 'ОК'.

Сада ће се наша производња регресијске анализе створити у новом радном листу, наводећи регресијску статистику, АНОВА, остатке и коефицијенте.

Излазно тумачење:

Регресијска статистика говори колико се једначина регресије уклапа у податке:

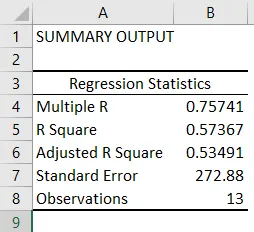
Мултипле Р је коефицијент корелације који мери снагу линеарног односа између две променљиве. Лежи између -1 и 1, а његова апсолутна вредност приказује снагу односа с великом вредношћу која указује на јачи однос, а мала вредност која означава негативну и нулту вредност која указује на никакав однос.
Р Скуаре је коефицијент одлучности који се користи као показатељ доброг фитања. Лежи између 0 и 1, а вредност близу 1 показује да је модел добро уклопљен. У овом случају, 0, 57 = 57% и-вредности се објашњава к-вредностима.
Прилагођени Р квадрат је Р квадрат подешен за број предиктора у случају вишеструке линеарне регресије.
Стандардна грешка приказује прецизност регресијске анализе.
Проматрања приказују број опажања модела.
Анова говори о нивоу променљивости унутар регресијског модела.

То се обично не користи за једноставну линеарну регресију. Међутим, „Ф-вредност значајности“ показује колико су наши резултати поуздани, чија вредност већа од 0, 05 сугерира да одаберете другог предиктора.

Коефицијенти су најважнији дио који се користи за изградњу регресијске једначине.

Дакле, наша регресијска једначина би била: и = 16.891 к - 355.32. То је исто као што је учињено методом 1 (расипање графикона са тренд-линијом).

Сада ако желимо да предвидимо просечне трошкове лечења када старосна доб износи 72 године:

Дакле, и = 16.891 * 72 -355.32 = 860.832

На тај начин можемо предвидјети вредности и за било које друге вредности к.

Остаци означавају разлику између стварних и предвиђених вредности.

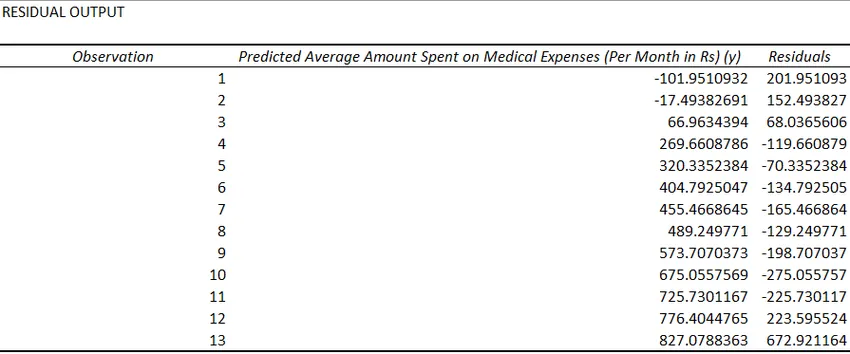
Последња метода регресије није толико често коришћена и захтева статистичке функције попут нагиба (), пресретања (), корела (), итд. За обављање регресијске анализе.

Ствари које треба запамтити о линеарној регресији у Екцелу

Регресијска анализа се обично користи да се види постоји ли статистички значајна веза између два скупа променљивих.
Користи се за предвиђање вредности зависне променљиве на основу вредности једне или више независних променљивих.
Кад год желимо да модел линеарне регресије уклопимо у групу података, тада треба пажљиво посматрати распон података као да користимо регресијску једнаџбу за предвиђање било које вредности изван овог распона (екстраполација), то може довести до погрешних резултата.

Препоручени чланци

Ово је водич за Линеарну регресију у Екцелу. Овде смо расправљали о томе како да направите Линеарну регресију у Екцелу заједно са практичним примерима и бесплатним екцел шаблоном. Можете и да прођете кроз друге наше предложене чланке -