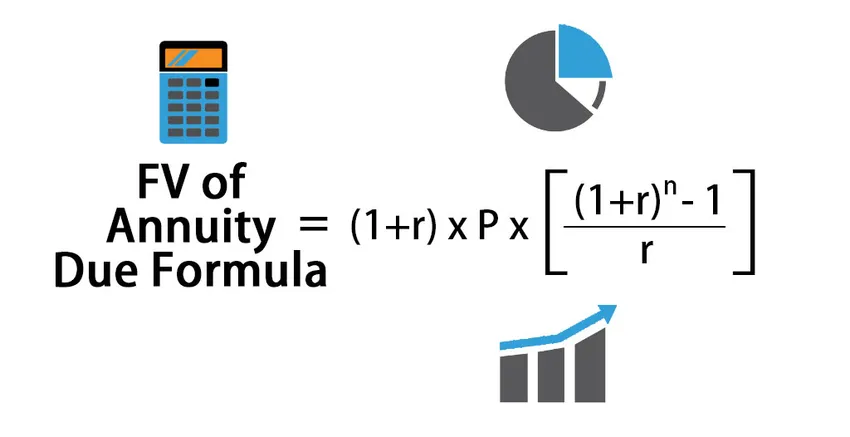
Будућа вредност формуле доспећа за ануитет (Садржај)
- Будућа вредност формуле за наплату ренте
- Примери будуће вредности доспећа формуле (са Екцел предлошком)
- Будућа вредност калкулатора формуле доспећа ануитета
Будућа вредност формуле за наплату ренте
Формула за израчунавање будуће вредности доспећа ануитета:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Где,
- П = Периодична уплата
- Р = стопа за период
- Н = Број периода
Примери будуће вредности доспећа формуле (са Екцел предлошком)
Узмимо пример да бисмо боље разумели израчунавање будуће вредности доспјећа по основу ануитета.
Овде можете преузети овај будући образац Екцел шаблона формуле за доспеће ануитета - Будућа вредност обрасца Екцел Формула ФормулаПример # 1
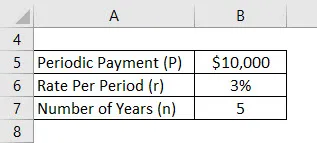
Претпоставимо да је Ананд депоновао 10.000 УСД годишње, а ефективна стопа коју његов рачун нуди је 3%. Сада Ананд жели да израчуна свој будући салдо после 5 година уз претпоставку првог депозита од данас па надаље.
Решење:
Будућа вредност доспећа за израчун ануитета израчунава се према нижој формули
ФВ од доспијећа ануитета = (1 + р) * П * (((1 + р) н - 1) / р)
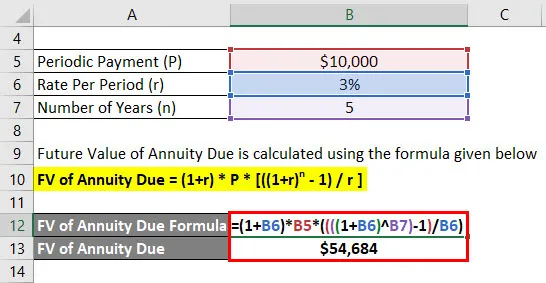
- ФВ оф Аннуити Дуе = (1+ 3%) * 10.000 УСД * ((((1 + 3%) 5) - 1) / 3%)
- ФВ од доспјела ануитета = 54, 684 $
Ананд ће након 5 година добити остатак од 54.684 долара.
Пример бр. 2
Претпоставимо да је Јагрити положио 8.000 УСД годишње, а ефективна стопа коју његов рачун нуди је 5%. Сада Јагрити жели израчунати свој будући салдо након 5 година уз претпоставку првог депозита од данас па надаље.

Решење:
Будућа вредност доспећа за израчун ануитета израчунава се према нижој формули
ФВ од доспијећа ануитета = (1 + р) * П * (((1 + р) н - 1) / р)
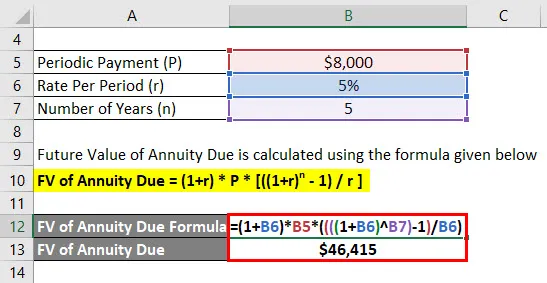
- ФВ оф Аннуити Дуе = (1+ 5%) * 8.000 УСД * ((((1 + 5%) 5) - 1) / 5%)
- ФВ од ренте = 46, 415 УСД
Јагрити ће након 5 година добити 46.415 $ будућег биланса.
Пример бр. 3
Претпоставимо да је Анандрити депоновао 20.000 УСД годишње, а ефективна стопа коју његов рачун нуди је 2%. Сада Анандрити жели да израчуна свој будући салдо после 5 година уз претпоставку првог депозита од данас па надаље.
Решење:
Будућа вредност доспећа за израчун ануитета израчунава се према нижој формули
ФВ од доспијећа ануитета = (1 + р) * П * (((1 + р) н - 1) / р)
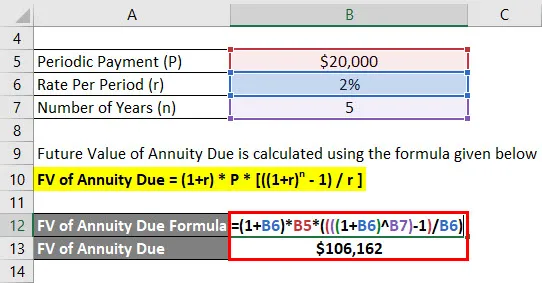
- ФВ од Аннуити Дуе = (1+ 2%) * $ 20, 000 * ((((1 + 2%) 5) - 1) / 2%)
- ФВ од доспјела ануитета = 1, 06, 162 УСД
Анандрити ће након 5 година добити будући биланс од 1, 06, 162 долара.
Објашњење
Да би израчунали крајњу вредност за низ новчаних токова или плаћања где се прва рата прими одмах, користимо Будућу вредност доспевања ануитета. Прва тренутна рата или исплата разликују ануитет због обичног ануитета. Непосредна или тренутна ануитета назива се ануитетом који доспева.
Израчунава вредност новчаних токова у будућем периоду. Употреба доспјелих ануитетних ануитета разликује се у реалним ситуацијама од садашње вриједности доспијећа ануитета. На пример, претпоставимо да компанија или појединац купују ануитет и данас су уплатили прву рату. Пример можемо да објаснимо даље, претпоставимо да компанија или појединац желе да откупе ануитет од било кога и да данас изврше прву уплату. Да бисмо израчунали цену коју треба платити у овој ситуацији, можемо да користимо садашњу вредност формуле за наплату ануитета. Међутим, ако желимо да израчунамо преостали салдо након што смо на рачуну сачували камате за 5 година и одлучили смо да данас плаћамо прву рату, у овом случају се користи будућа вредност ануитета. Доспјела ануитета може се објаснити као врста ренте код које се новчани токови појављују на почетку сваког периода. Због напредне природе новчаних токова, сваки новчани ток подлеже дејству компензације за сваки наредни период у случају да се упореди са обичном ануитетом. Будућа вредност обичног ануитета нижа је од будуће вредности ануитета, јер будућа вредност ануитета добија периодичну камату од фактора један плус.
Релевантност и употреба будуће вредности доспећа ануитета
Да разумемо значење вредности будућности и ануитета који се доспевају одвојено. Будућа вредност може се објаснити као укупна вредност за износ готовине који ће се плаћати у будућности на одређени датум. А доспјели ануитет може се објаснити као низ исплате који се врше на почетку сваког периода у редовном редоследу. Стога се будућа вредност доспећа ануитета може објаснити као укупна вредност одређеног датума у будућности за низ систематских / периодичних плаћања где се плаћања врше на почетку сваког периода. Ова врста трансакције и такав ток плаћања могу се видети на рачуну корисника пензијског плана. Укупна вредност је износ до кога ће серија плаћања извршених у будућем датуму порасти, како се претпоставља одређени износ камате, а зарада постепено расте у одређеном периоду. Израчун будуће вредности обичног ануитета идентичан је овоме, али једина је разлика што додајемо додатни период плаћања који се врши на почетку.
Будућа вредност калкулатора формуле доспећа ануитета
Можете користити следећи калкулатор будуће вредности доспећа ануитета
| П | |
| р | |
| н | |
| Будућа вредност формуле за наплату ренте | |
| Будућа вредност формуле због доспјећа = | (1 + р) * П * (((1 + р) н - 1) / р) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Препоручени чланци
Ово је водич за будућу вредност формуле за плаћање ануитета. Овде смо разговарали о томе како израчунати будућу вредност доспећа уз практичне примере. Такође нудимо калкулатор будуће вредности доспијећа за ануитет са надоградивим предлошком Екцел. Такође можете погледати следеће чланке да бисте сазнали више -
- Водич за временску вредност новца Формуле
- Примери формуле садашњег фактора вредности
- Калкулатор за формулу односа података
- Формула за степен оперативног утјецаја