
Р - Квадратна формула (Садржај)
- Р - квадратна формула
- Примери Р - квадратне формуле (са Екцеловим предлошком)
- Р - квадратни калкулатор
Р - квадратна формула
Формула Р-квадрата је такође позната као коефицијент утврђивања, она је статистичка мера која одређује повезаност између перформансе инвеститора и приноса или перформанси референтног индекса. У основи показује који степен успешности акција или портфеља може се приписати одређеном референтном индексу. Ова формула се мало разликује од корелације променљиве јер формула корелације приказује однос између зависне и независне променљиве, док са друге стране, Р-квадратна формула показује у којој мери варијанца једне променљиве објашњава варијанцу друге променљиве .
Формула за Р - квадрат је дата од:
R – Squared = 1 – (Sum of First Errors / Sum of Second Errors)
Примери Р - квадратне формуле (са Екцеловим предлошком)
Узмимо пример да бисмо боље разумели израчунавање Р - квадрата.
Можете преузети овај Р - квадратни образац формуле овде - Р - образац квадратног формулаПример # 1
Размотрите следеће информације и израчунајте Р квадрат.
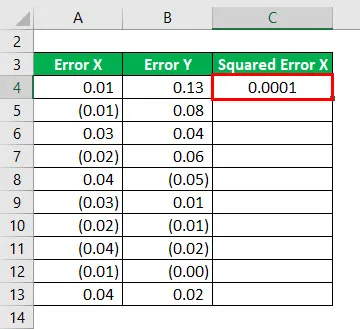
Квадрат грешке Кс ће се израчунати као:
Резултат ће бити наведен у наставку.
Квадрат грешке Кс за све податке као што је дато у наставку.
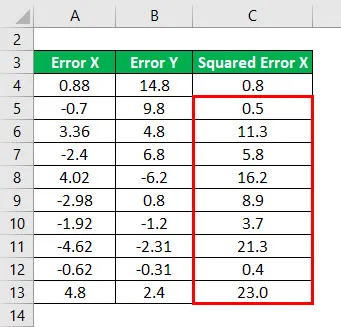
Слично томе, за све податке морамо израчунати квадрат грешке И.
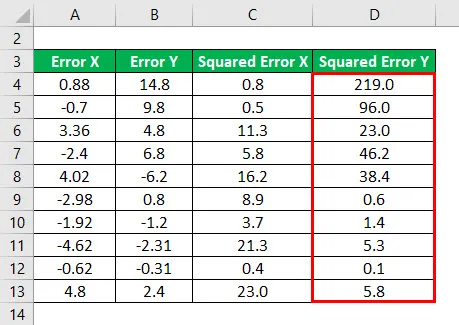
Р - Квадрат се израчунава према доњој формули
Р - квадрат = 1 - (збир првих грешака / збир других грешака)
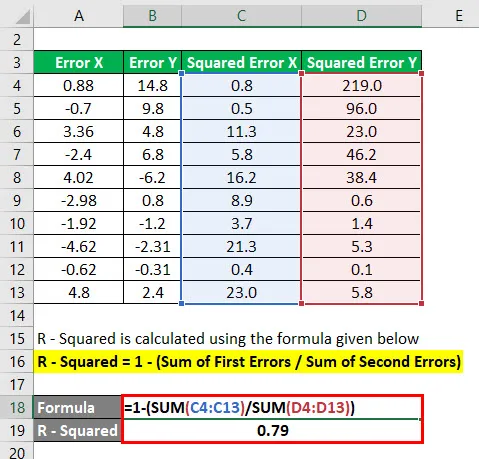
Овде смо прво уклонили грешку следећих тачака и извршили суму горе наведених проблема. Након тога, зброј прве грешке се дели са збројем друге грешке и одузима се са 1.
Р-квадрат је у опсегу од 0 до 1. Р-квадрат са 1 или 100% означава да су сва кретања у индексу у потпуности објашњена покретима у референтном индексу.
Пример бр. 2
Размотрите следеће информације и израчунајте Р квадрат.
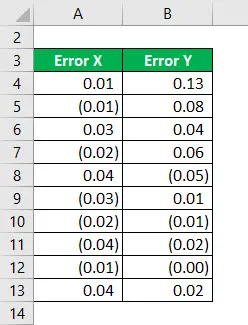
Квадрат грешке Кс ће се израчунати као:
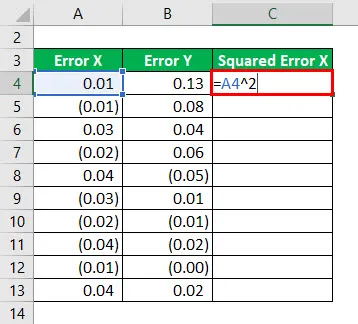
Резултат ће бити наведен у наставку.
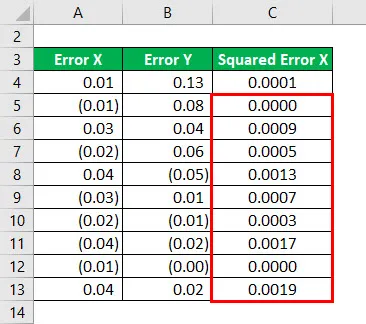
Квадрат грешке Кс за све податке као што је дато у наставку.
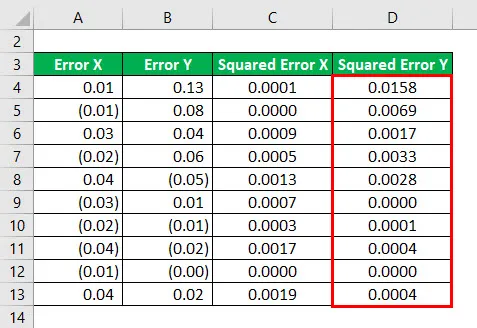
Слично томе, за све податке морамо израчунати квадрат грешке И.
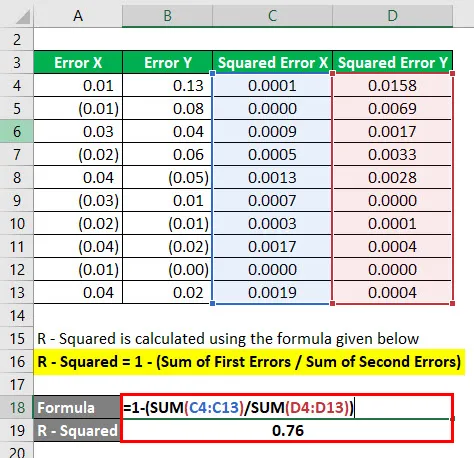
Р - Квадрат се израчунава према доњој формули
Р - квадрат = 1 - (збир првих грешака / збир других грешака)
Пример бр. 3
Размотрите следеће информације и израчунајте Р квадрат.
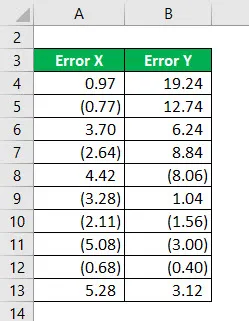
Квадрат грешке Кс ће се израчунати као:
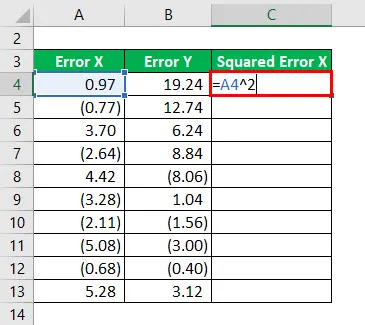
Резултат ће бити наведен у наставку.
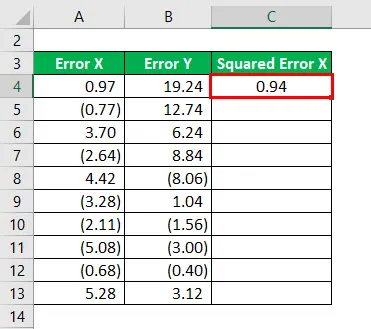
Квадрат грешке Кс за све податке као што је дато у наставку.
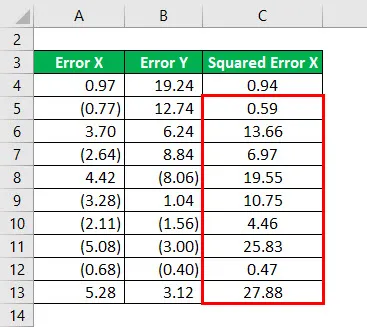
Слично томе, за све податке морамо израчунати квадрат грешке И.
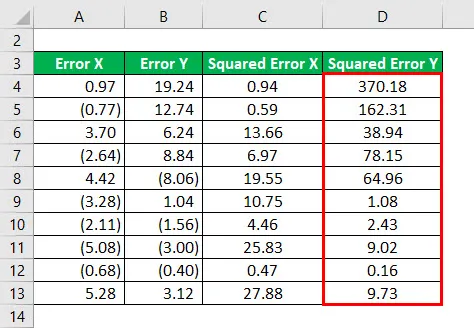
Р - Квадрат се израчунава према доњој формули
Р - квадрат = 1 - (збир првих грешака / збир других грешака)
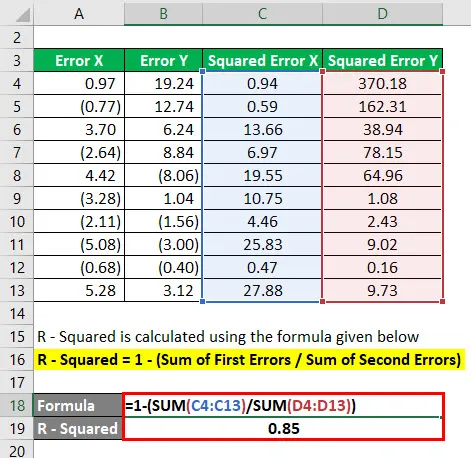
Релевантност и употреба
- Ову формулу широко користе менаџери портфеља и менаџери фондова као мера која говори о томе како кретања средстава корелирају са референтним индексом.
- Ова формула се такође користи у берзанској индустрији која брокеру или инвеститору говори колико добро акције корелирају са укупним кретањем тржишта.
- Ова формула има своја ограничења јер не може процијенити да ли су процјене коефицијента и предвиђања пристрасни или не, стога требате процијенити преостале парцеле.
- Тамо где Р - квадрат није добар модел за упоређивање квалитета две променљиве, а подешени Р-квадрат се користи већином времена за обављање вишеструких линеарних регресија.
- Низак или висок Р-квадратни број не може бити увек добар или лош јер кориснику не говори о поузданости модела.
- Ако корисник има ниску вредност Р-квадрата, али независне променљиве су статистички значајне, корисник може и даље да изводи важне закључке о односу између променљивих.
Р - квадратни калкулатор
Можете користити следећи Р - квадратни калкулатор
| Збир првих грешака | |
| Збир других грешака | |
| Р - квадратна формула | |
| Р - квадратна формула = | 1 - (збир првих грешака / збир других грешака) |
| = | 1 - (0/0) = 0 |
Препоручени чланци
Ово је био водич за Р - Скуаред Формула. Овде ћемо расправити како израчунати Р - квадрат заједно са практичним примерима. Такође нудимо калкулатор Р - квадрата са довнлоад-офом екцел шаблона. Такође можете погледати следеће чланке да бисте сазнали више -
- Водич за очекивану формулу повратка
- Како израчунати ПЕГ однос?
- Примери формуле коефицијента солвентности
- Калкулатор за формулу коефицијента левера