
Коефицијент формуле одређивања (Садржај)
- Формула
- Примери
Који је коефицијент формуле одређивања?
У статистици, коефицијент одређивања, који се такође назива Р2 је алат који одређује и процењује способност статистичког модела да објасни и предвиди будуће исходе. Другим речима, ако у моделу имамо зависну променљиву и и независну променљиву к, тада Р2 помаже у одређивању варијације и променом к. То је један од кључних резултата регресијске анализе и користи се када желимо да предвидимо будућност или тестирамо неке моделе са сродним информацијама. Вредност Р2 лежи између 0 и 1 и већа вредност Р2, боље ће бити предвиђање и снага модела. Р2 је врло сличан коефицијенту корелације, јер коефицијент корелације мери директну повезаност две променљиве. Р2 је у основи квадрат коефицијента корелације.
Формула за коефицијент одлучности:
Постоји више формула за израчунавање коефицијента одређивања:
- Коришћење коефицијента корелације:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Где:
- Кс - Точке података у скупу података Кс
- И - Подаци података у скупу података И
- Кс м - Средња вредност скупа података Кс
- И м - Средња вриједност скупа података И
Тако
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Користећи регресијске излазе
Коефицијент утврђивања (Р 2 ) = Објашњена варијација / Укупна варијација
Коефицијент утврђивања (Р2) = МСС / ТСС
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Где:
- ТСС - Укупан збир квадрата = Σ (Ии - Им) 2
- МСС - Моделни зброј квадрата = Σ (И - Им) 2
- РСС - Преостали збир квадрата = Σ (Ии - И ^) 2
И је предвиђена вредност модела, Ии је и вредност, а Им је средња вредност
Примери коефицијента формуле одређивања (са Екцеловим предлошком)
Узмимо пример како бисмо боље разумели израчунавање коефицијента одлучности.
Овде можете преузети овај коефицијент обрасца Екцел шаблона формуле одређивања овде - Коефицијент Формуле Шаблон Формуле за одређивањеКоефицијент формуле одређивања - пример бр. 1
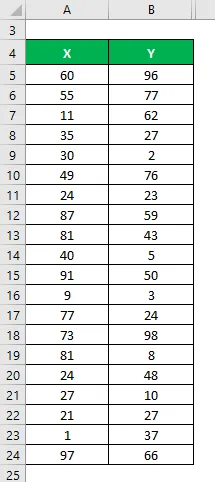
Рецимо да имамо два скупа података Кс&И и сваки садржи 20 случајних података. Израчунајте коефицијент утврђивања за скуп података Кс&И.
Просек се израчунава као:
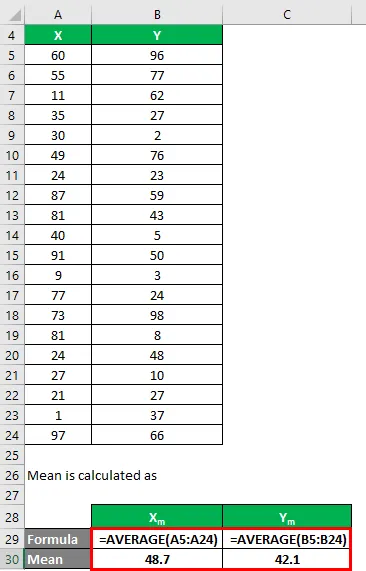
- Средња вредност скупа података Кс = 48.7
- Средња вредност скупа података И = 42.1
Сада морамо израчунати разлику између података и средњих вредности.
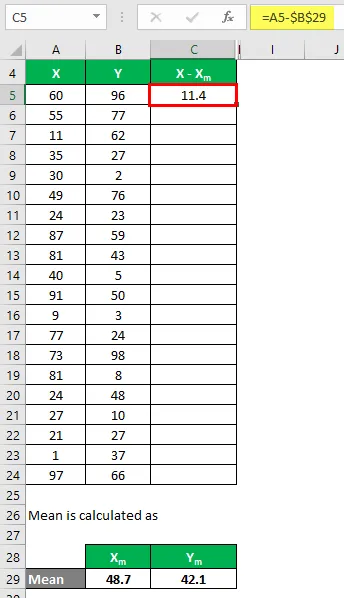
Слично томе, израчунајте за све скупове података Кс.
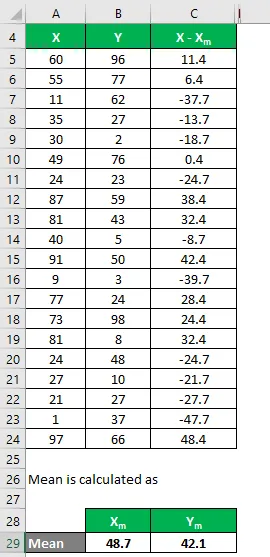
Слично томе, израчунајте и за скуп података И.

Израчунајте квадрат разлике за оба скупа података Кс и И.
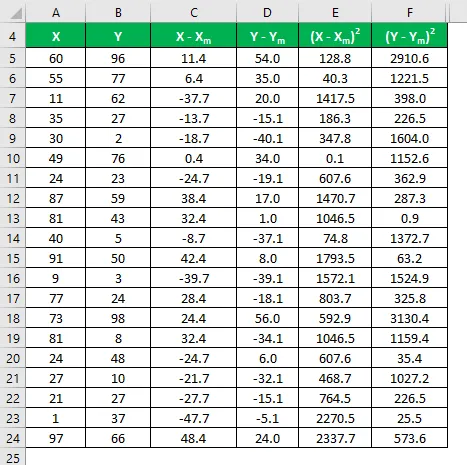
Помножите разлику у Кс са И.
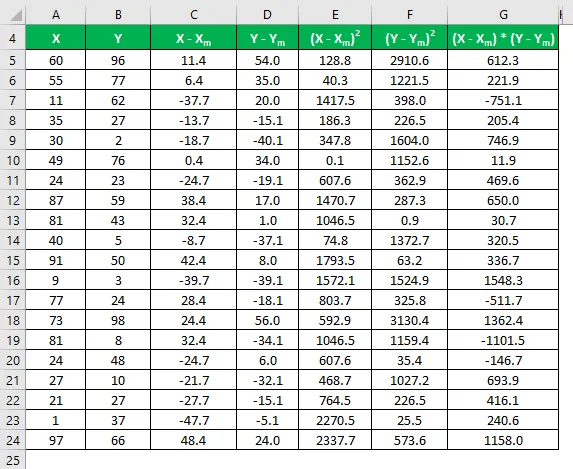
Коефицијент корелације израчунава се помоћу доле наведене формуле
Коефицијент корелације = Σ ((Кс - Кс м ) * (И - И м )) / √ (Σ (Кс - Кс м ) 2 * Σ (И - И м ) 2 )
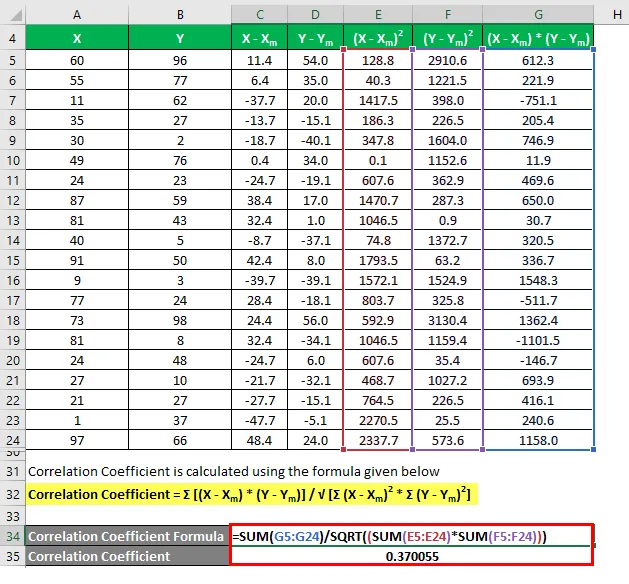
Коефицијент утврђивања израчунава се користећи ниже формулу
Коефицијент утврђивања = (коефицијент корелације) 2
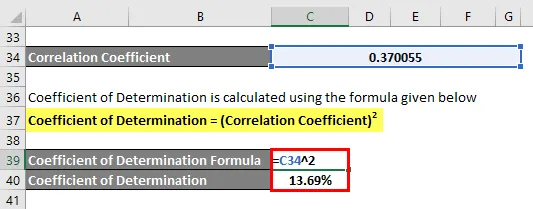
Коефицијент одлучности = 13, 69%
Коефицијент формуле одређивања - пример бр. 2
Рецимо да сте инвеститор веома ризичан и желите да уложите новац на берзу. Нисте сигурни у које акције треба уложити, а ни апетит за ризик је низак. На тај начин желите инвестирати у акције које су сигурне и могу опонашати перформансе индекса. Ваш пријатељ, који је активни инвеститор, уврстио је у ужи избор 3 акције за вас на основу њихових основних и техничких информација и желите да одаберете две акције међу ове три.
Такође сте прикупили информације о њиховим историјским повратима у последњих 15 година.
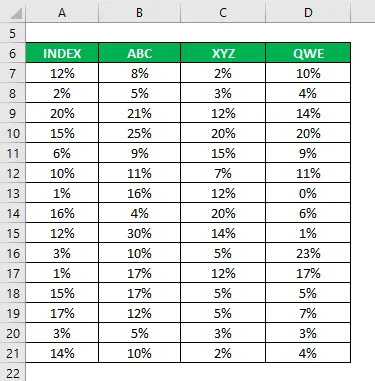
Корелациони коефицијент се израчунава помоћу екцел формуле
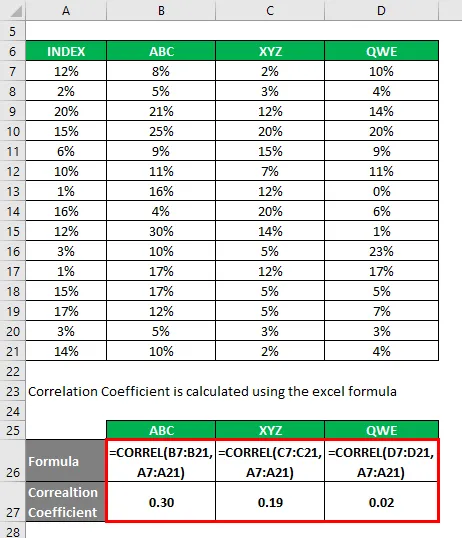
Коефицијент утврђивања израчунава се користећи ниже формулу
Коефицијент утврђивања = (коефицијент корелације) 2
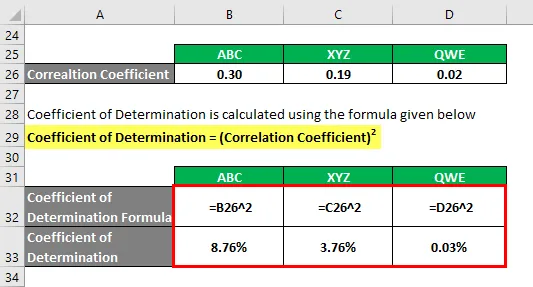
На основу информација, изабрати ћете акције АБЦ и КСИЗ за улагање, јер они имају највећи коефицијент одређивања.
Објашњење
Коефицијент одређивања, као што је горе објашњено, је квадрат корелације између два скупа података. Ако је Р2 0, то значи да нема корелације и независна варијабла не може предвидети вредност зависне променљиве. Слично томе, ако је његова вредност 1, то значи да ће независна променљива увек бити успешна у предвиђању зависне променљиве. Али постоје и нека ограничења. Иако нам говори о корелацији између два скупа података, он нам не говори је ли та вриједност довољна или не.
Такође, велика вредност Р2 не значи увек да две променљиве имају јаке везе и да може бити флуке. На пример: Рецимо да вредност Р2 између броја аутомобила који се продају у току године и броја продатих кутија за сладолед у години износи 80%. Али нема везе између ово двоје. Стога треба бити врло опрезан док користите Р2 и прво разумјети податке, а затим примијенити методу
Релевантност и употреба коефицијента формуле одређивања
Постоје многе практичне примене Р2. На пример, Р2 инвеститори често користе да упореде перформансе свог портфеља са тржиштем и покушају да предвиде и будуће правце. Слично томе, хедге фондови помоћу Р2 помажу им да моделирају ризик на својим моделима. Али на крају се исход заснива на чистим бројевима и статистикама, који понекад могу бити погрешни. Као што је горе поменуто, прво треба проверити да ли излаз Р2 има смисла у стварном животу или не.
Препоручени чланци
Ово је водич за Коефицијент Формуле за Одређивање. Овде смо расправљали о томе како израчунати коефицијент одлучности заједно са практичним примерима и довнлоад-ом Екцел шаблона. Такође можете погледати следеће чланке да бисте сазнали више -
- Водич за Формула за тржишни ризик Премиум
- Примери формуле покривености покривености
- Калкулатор за формулу трошка на основу активности
- Како израчунати однос информација користећи формулу?