Коефицијент формуле варијације - Прорачун са Екцел шаблоном

Коефицијент формуле варијације (Садржај)

• Формула
• Примери

Који је коефицијент формуле варијације?

У статистици, коефицијент варијације који се такође назива ЦВ је алат који нам помаже да одредимо како се тачке података у скупу података распоређују око средње вредности. У основи, прво се цртају све тачке података, а затим се користи коефицијент варијације за мерење дисперзије тих тачака једна од друге и средње вредности. Тако нам помаже у разумевању података и такође да видимо образац који формирају. Израчунава се као однос стандардног одступања скупа података према средњој вредности. Већи коефицијент варијације значи да постоји већи ниво дисперзије података око средње вредности. Слично томе, нижа је вредност коефицијента варијације, мања је дисперзија и прецизнији ће бити резултати. Чак и ако се средина две серије података знатно разликује, коефицијент варијације је врло користан за упоређивање степена варијације од једне серије података до друге.

Формула за коефицијент варијације је дата од:

Coefficient of Variation = Standard Deviation / Mean

Кораци за израчунавање коефицијента варијације:

Корак 1: Израчунајте средину скупа података. Средња вредност је просек свих вредности и може се израчунати тако да се узме зброј свих вредности и затим подели са бројем података.

Корак 2: Затим израчунајте стандардну девијацију скупа података. То је мало захтјеван процес. Одступање стандарда може се израчунати као: √ (Σ (Кс _и - Кс _м ) ² / (н - 1)) . Кс _и је тачка података и Кс _м је средина скупа података. Алтернативно, стандардну девијацију у екцелу можемо пронаћи и користећи СТДЕВ.С () функцију.

Корак 3: Поделите стандардну девијацију на средњу вредност да бисте добили коефицијент варијације.

Примери коефицијента формуле варијације (са Екцеловим предлошком)

Узмимо пример како бисмо боље разумели израчунавање коефицијента варијације.

Овде можете преузети овај коефицијент обрасца Екцел шаблона формула варијације овде - Коефицијент обрасца варијације Формула Екцел

Коефицијент формуле варијације - Пример 1

Рецимо да имамо два скупа података А&Б и сваки садржи 20 случајних података. Израчунајте коефицијент варијације за скуп података Кс&И.

Решење:

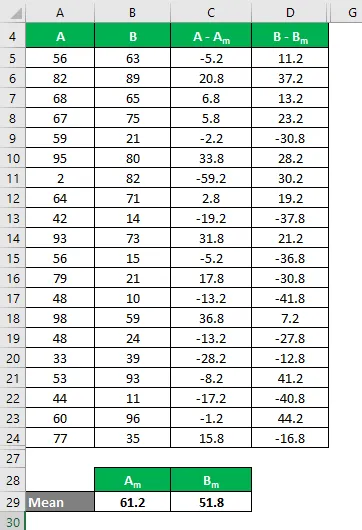
Просек се израчунава као:

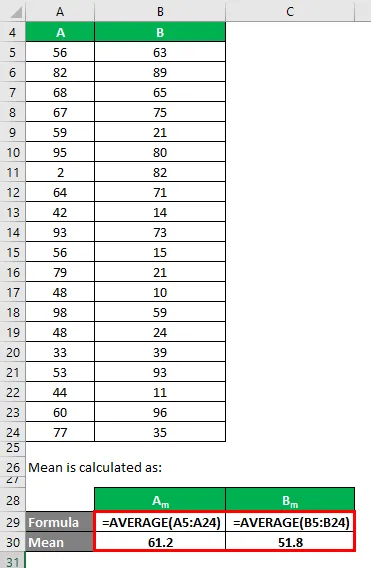
• Средња вредност скупа података А = 61.2
• Средња вредност скупа података Б = 51.8

Сада морамо израчунати разлику између података и средњих вредности.

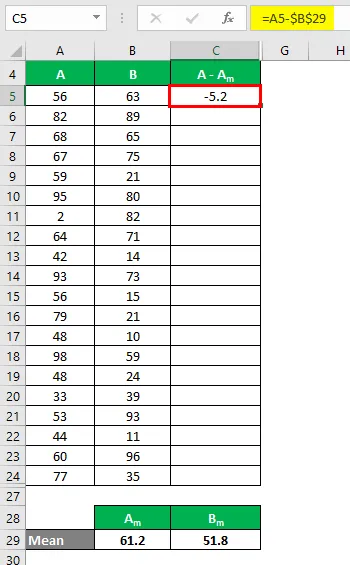
Слично томе, израчунајте за све вредности скупа података А.

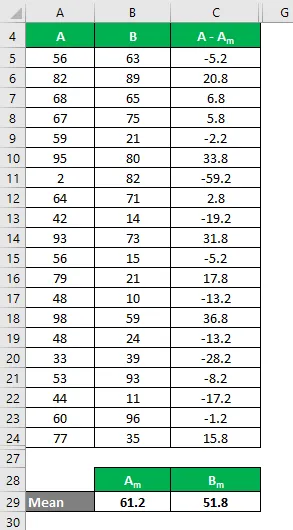
Слично томе, израчунајте за све вредности скупа података Б.

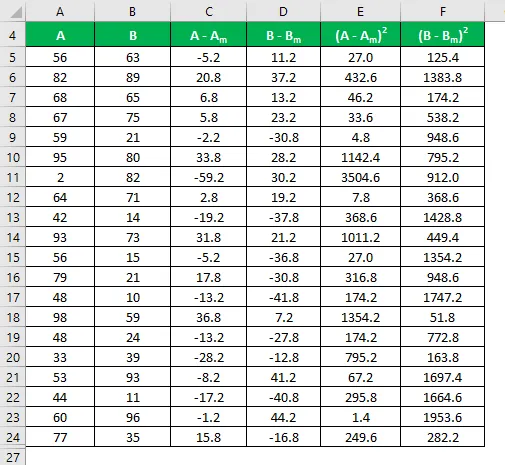
Израчунајте квадрат разлике за оба скупа података А и Б.

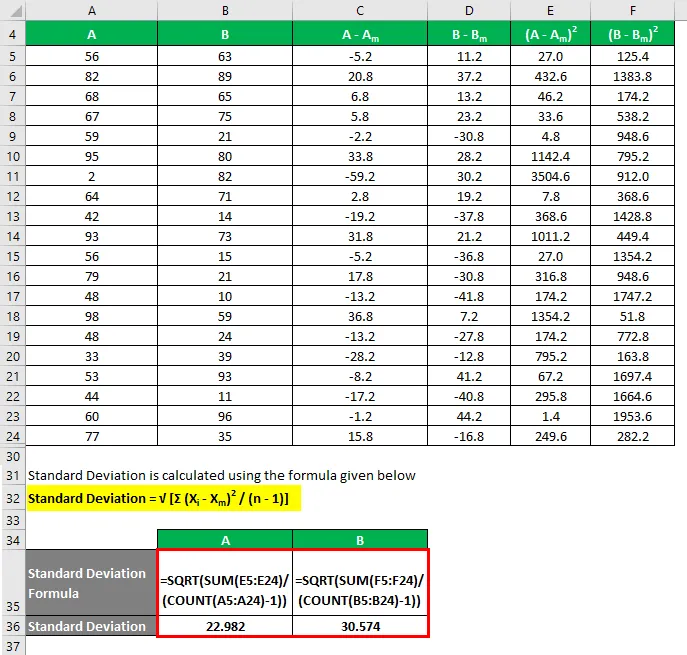
Стандардно одступање се израчунава на основу доље наведене формуле

Стандардно одступање = √ (Σ (Кс _и - Кс _м ) ² / (н - 1))

Коефицијент варијације се израчунава коришћењем доле наведене формуле

Коефицијент варијације = стандардно одступање / средња вредност

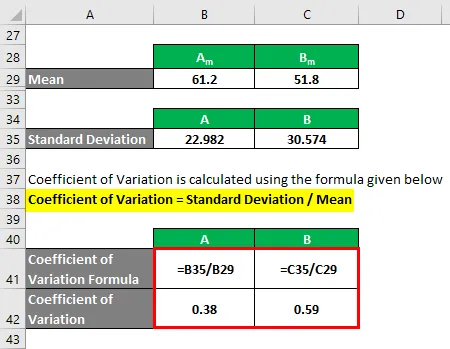
• Коефицијент варијације А = 22, 982 / 61, 2 = 0, 38
• Коефицијент варијације Б = 30, 574 / 51, 8 = 0, 59

Дакле, ако овде видите, Б ​​има већи коефицијент варијације од А, што значи да су тачке података Б више дисперговане од А.

Коефицијент формуле варијације - пример бр. 2

Рецимо да сте инвеститор веома ризичан и желите да уложите новац на берзу. Пошто је апетит за ризиком низак, желите да инвестирате у сигурне акције које имају нижи стандардни одступање и коефицијент варијације. Ушли сте у ужи избор 3 акције на основу њихових основних и техничких информација и желите да одаберете 2 акције. Такође сте прикупили информације о њиховим историјским повратима у последњих 15 година.

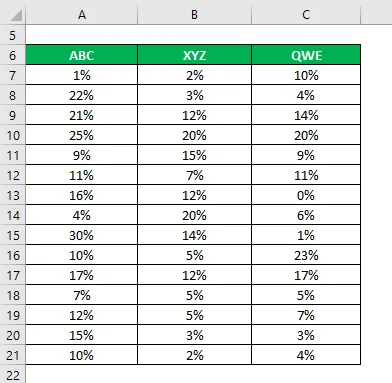
Решење:

Просек се израчунава као:

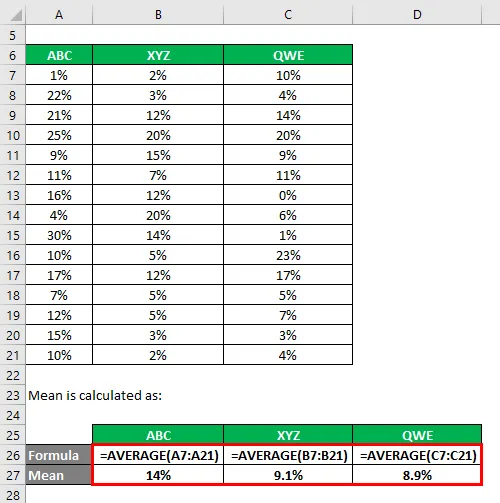
Стандардно одступање се израчунава помоћу екцел формуле

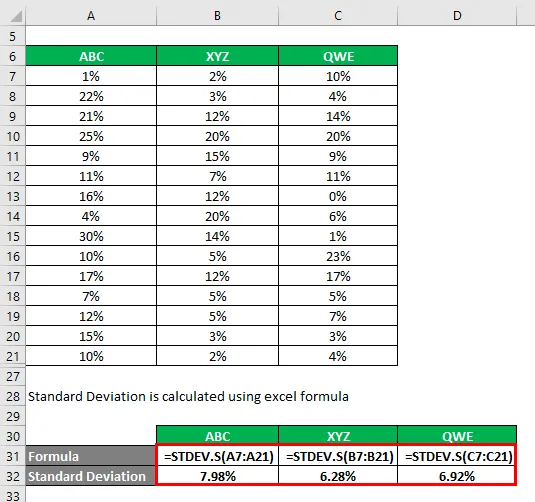
Коефицијент варијације се израчунава коришћењем доле наведене формуле

Коефицијент варијације = стандардно одступање / средња вредност

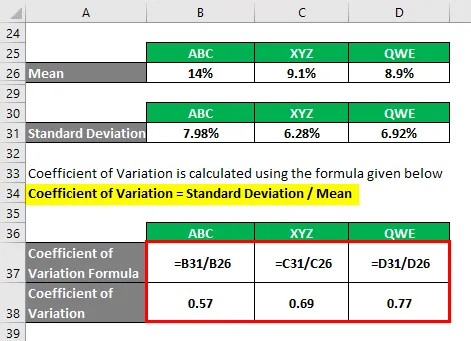
• Коефицијент варијације АБЦ = 7, 98% / 14% = 0, 57
• Коефицијент варијације КСИЗ = 6, 28% / 9, 1% = 0, 69
• Коефицијент варијације КВЕ = 6, 92% / 8, 9% = 0, 77

На основу информација, изаберите дионице АБЦ и КСИЗ за улагање, јер имају најмањи коефицијент варијације.

Објашњење

Пошто је коефицијент варијације мерило ризика, помаже у мерењу волатилности цена акција и других финансијских инструмената. Такође помаже инвеститорима и аналитичарима да упореде ризике повезане са различитим потенцијалним улагањима.

Коефицијент варијације сличан је стандардној девијацији, али стандардно одступање двије варијабле не може се упоредити са корисним. Али, коришћење стандардне девијације и средње вредности, релативно поређење чини смисленијим. Постоји и ограничење коефицијента варијације. Претпоставимо да је средња вредност скупа података једнака нули. У том случају овај алат ће постати неефикасан. И не само то, ако имамо скуп података који има много позитивних и негативних вредности, коефицијент варијације постаје врло проблематичан. Стога је корисније само код скупова података који имају исти знак плус-минус.

Релевантност и употреба коефицијента формуле варијације

Коефицијент варијације има релевантност у многим другим областима осим статистике. На пример, у области финансија, коефицијент варијације је мерило ризика. Слично је са стандардном девијацијом јер се такође користи као мјера ризика, али разлика је у томе што је коефицијент варијације бољи показатељ релативног ризика. На пример, рецимо очекивани повраћај А од 15% и очекивани поврат Б од 10%, а А стандардно одступање од 10%, док Б има стандардно одступање од 5%. Да бисте изабрали бољу инвестицију, може се користити коефицијент варијације. Коефицијент варијације А је 10/15 = 0, 666, а коефицијент варијације Б је 5/10 = 0, 5. Дакле, Б је боља инвестиција од А.

Препоручени чланци

Ово је водич за Коефицијент формуле варијације. Овде смо расправљали о томе како израчунати коефицијент варијације користећи формулу заједно са практичним примерима и довнлоад-ом Екцел шаблона. Такође можете погледати следеће чланке да бисте сазнали више -

1. Шта је прилагођена Р квадратна формула?
2. Примери коефицијента формуле одређивања
3. Како израчунати коефицијент корелације помоћу формуле?
4. Формула коварианце са предлошком Екцел