Екцел НОРМСИНВ (Садржај)
- Увод у Екцел НОРМСИНВ
- Како се користи НОРМСИНВ формула у Екцелу?
Увод у Екцел НОРМСИНВ
Функција инверзне нормалне кумулативне дистрибуције у екцелу је важан алат који враћа инверзну нормалну кумулативну дистрибуцију за дату вредност вероватноће, тј. Обично враћа инверзу стандардне нормалне кумулативне дистрибуције (која има средњу нулу и стандардну девијацију од једне) Функција НОРМ.С.ИНВ први пут је уведена у верзији Мицрософт екцел 2010, која је ажурирана верзија НОРМСИНВ функције у екцелу 2013 и најновијој верзији. НОРМСИНВ функција се углавном користи у анализи дуга и финансија.
Синтакса програма Екцел НОРМСИНВ

Расправа:
Вероватноћа - што није ништа друго него вероватноћа одговара нормалној дистрибуцији.
Како се користи НОРМСИНВ формула у Екцелу?
У Мицрософту се издваја НОРМСИНВ уграђена функција је категорисана у статистичку функцију која је приказана на слици испод (где ће израчунати инверзију нормалне кумулативне дистрибуције за дату вероватноћу).
- Идите на мени Формула.
- Кликните на Више функција као што је приказано на слици испод.

- Изаберите категорију статистика под којом ћемо пронаћи функцију НОРМ.ДИСТ као ниже.
Пример # 1 - Коришћење НОРМ.ДИСТ и НОРМСИНВ
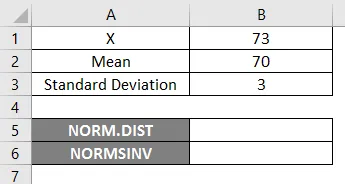
Да бисмо користили функцију НОРМ.ДИСТ, почнимо с једноставним примером где треба да сазнамо студентске оцене, претпоставимо да имамо разредни испит са просечном оценом 70 тј. Му = 70 и стандардна девијација у класи 3 бода, тј. Сигма = 3 овде морамо да откријемо колика је вероватноћа да су студенти добили оцене 73 или испод тј. П (Кс <= 73). Па да видимо како да сазнамо вероватноћу помоћу функције НОРМ.ДИСТ.
- Кс = 3
- Средња вредност = 70
- Стандардно одступање = 3
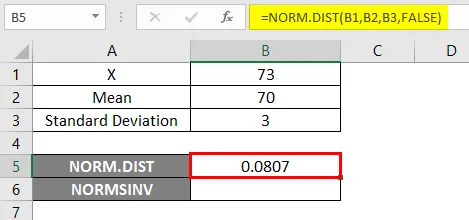
- Примените НОРМ.ДИСТ функцију на следећи начин.
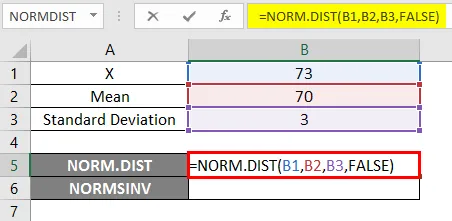
- Ако применимо горњу НОРМ.ДИСТ функцију, добићемо вероватноћу 0, 0807.
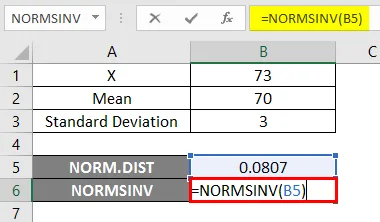
- Сада примените НОРМСИНВ функцију да бисте сазнали инверзу нормалне кумулативне дистрибуције као што је приказано у наставку.
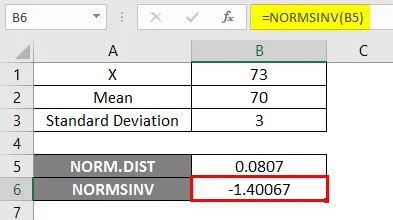
Резултат -
На доњем резултату можемо видети да смо добили негативне вредности -1.40067 за дату вероватноћу, тј. Обратну нормалну кумулативну дистрибуцију.
Пример # 2 - Средње и тачно стандардно одступање
Погледајмо још један пример са подацима заснованим на кривуљи, тако да можемо упознати средњу и тачну стандардну девијацију.
- Средња вредност = 7
- Стандардно одступање = 1.3
- Стандардни пораст одступања као -3

- Да бисмо добили кривуљу звона, морамо додати 0, 1 на прираст стандардног одступања где су подаци приказани доле.
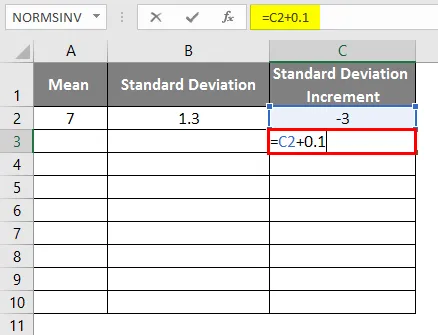
- Након примене формуле резултат је као што је приказано испод.
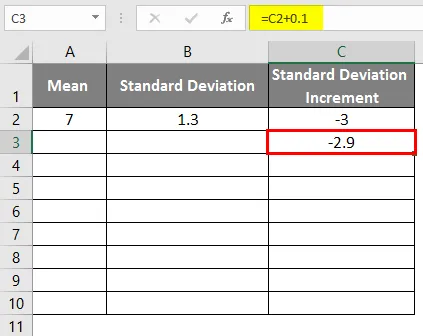
- Превуците вредности да добијемо више вредности док не добијемо позитивне вредности тако да ћемо добити леву криву.
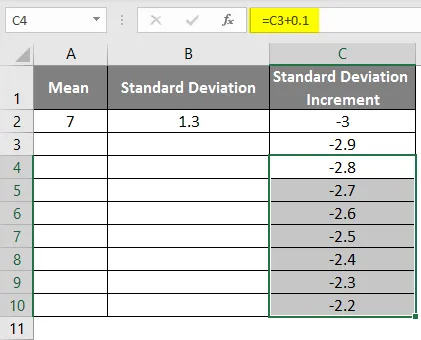
- Да бисмо добили праву кривуљу морамо формулу применити као = средње-стандардно одступање * 3, тако да ћемо добити тачне криве.
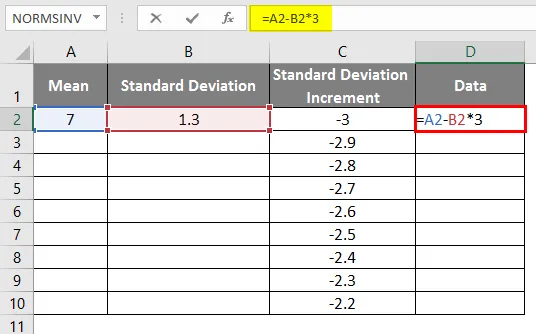
- Након употребе формуле резултат је приказан доле.
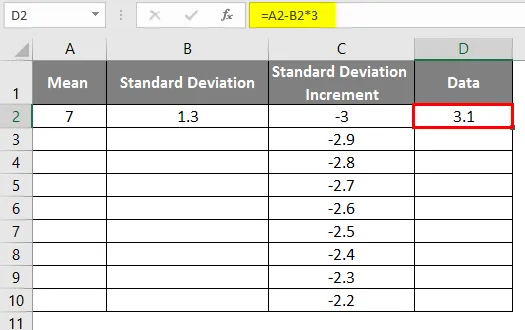
- Као и у горњим подацима за увећање стандардне девијације да бисмо добили леву кривуљу, вредности смо увећали за 0, 1
- Исти сценариј се користи применом формуле као = 3.1 + СТАНДАРДНО ДЕВИАТИОН / 10 за добијање повећања кривуље 0, 1
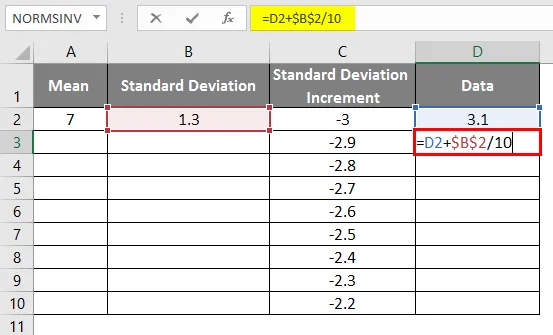
- Након употребе формуле резултат је приказан доле.

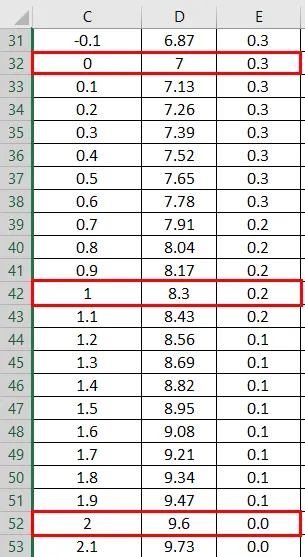
- Превуците вредности да бисте добили тачан резултат који је приказан на слици испод.
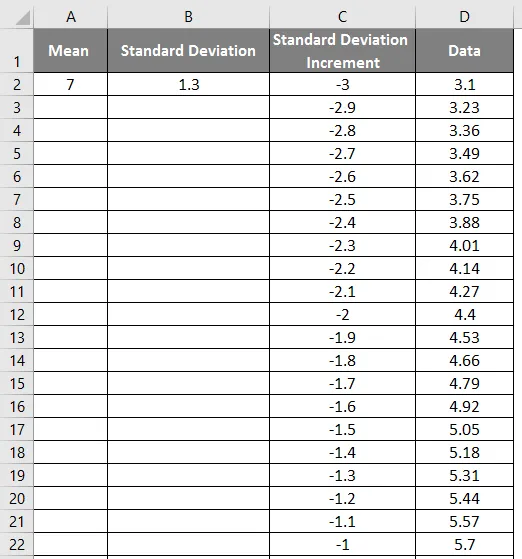
- Сада примените нормалну функцију дистрибуције са формулом = НОРМ.ДИСТ (вредност ДАТА, средња вредност, стандардна девијација, лажна).
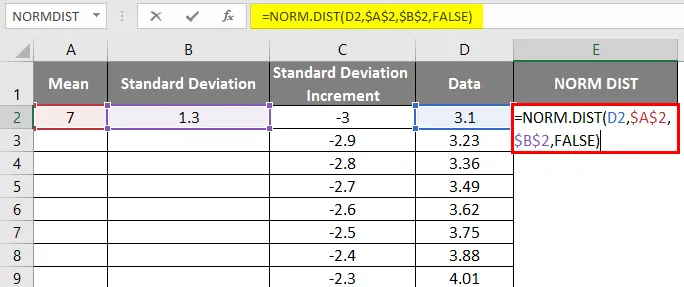
- Добићемо следећи резултат на следећи начин.
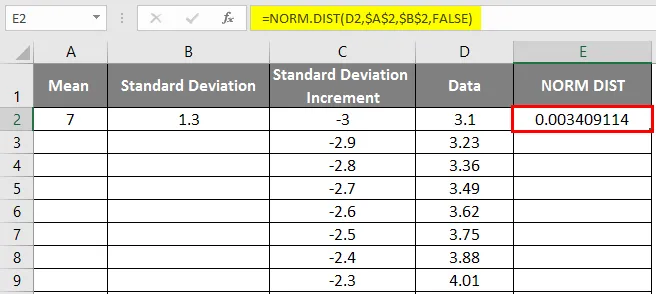
- Превуците вредности да бисте добили тачан резултат који је приказан доле.
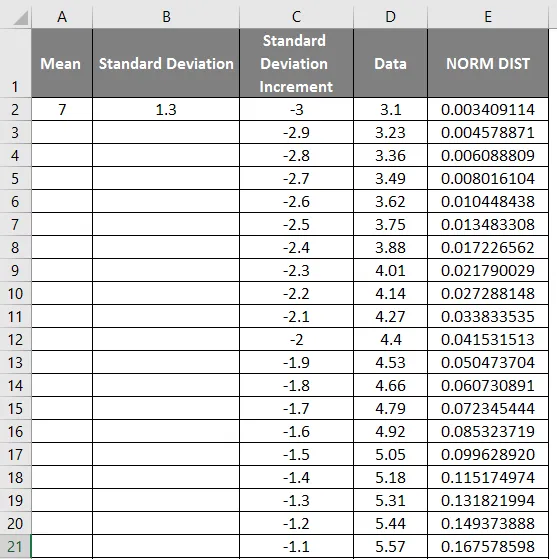
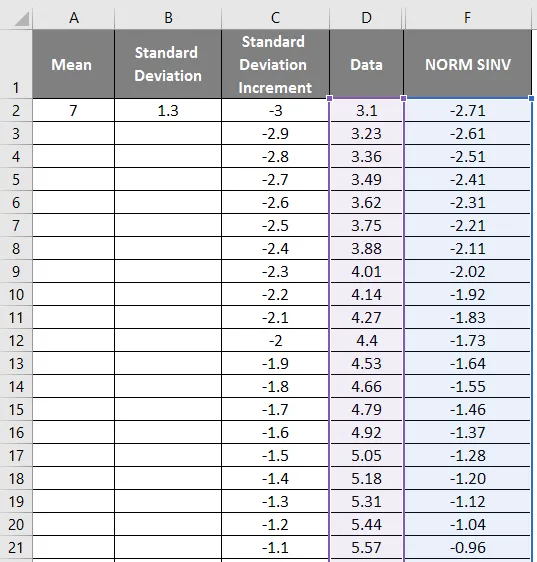
- Као што видимо на горњем снимку слике, израчунали смо НОРМАЛну дистрибуцију од средње и стандардне девијације. Сада да видимо шта ће бити обратно НОРМАЛ дистрибуцији применом НОРМСИНВ-а који је приказан у наставку.
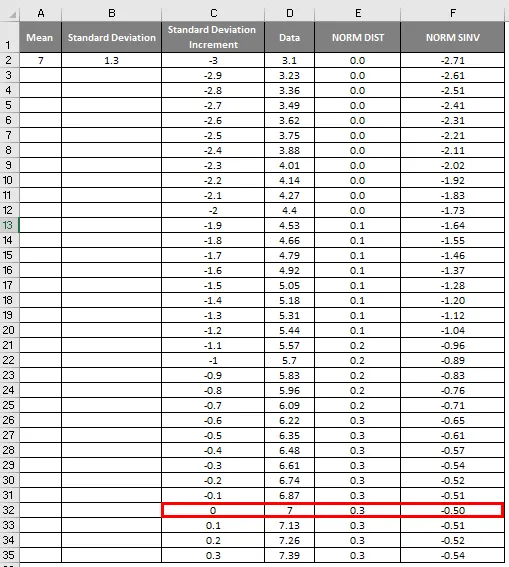
- Овде можемо видети да вредност Зеро (0) има стандардно одступање као 7.

Применом раштрканог графикона да бисте погледали како изгледа лева и десна крива.
- Прво одаберите податке и ступац Нормал.
- Идите на картицу Уметање и одаберите раштркани граф на следећи начин.
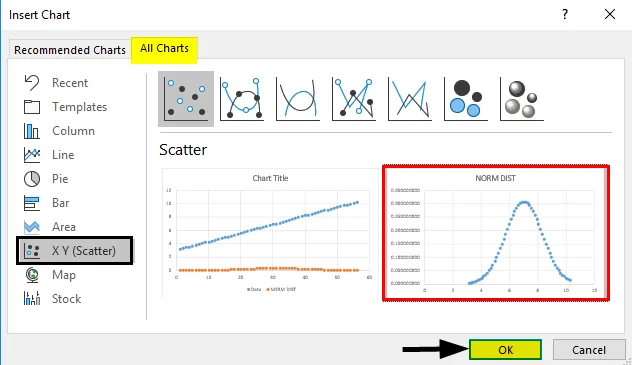
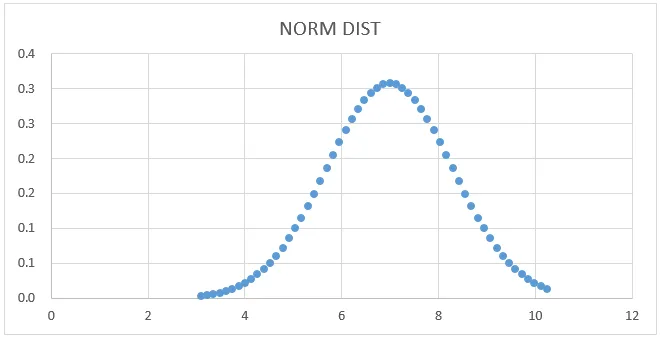
- Добићемо графикон испод криве као што је приказано у наставку.
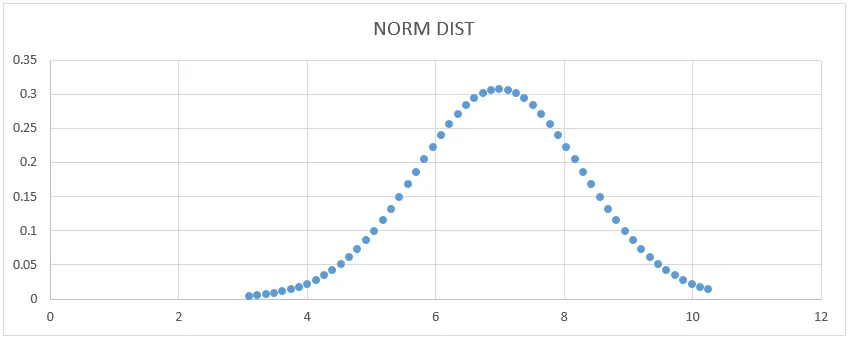
Овде можемо видети да средња вредност 7 има стандардни облик девијације где то можемо показати цртањем правих линија која ће га представити.
- Средња вредност = 7
- 1 –Стандардно одступање указује на 68% података.
- 2 –Стандардно одступање указује на 95% података.
- 3 - Стандардно одступање указује на 99, 7% података.
Нормални распоред расподјеле:
Графикон НОРМСИНВ:
Сада са горње слике изаберите колону података и НОРМ СИНВ да бисте добили доњи графикон на следећи начин.
- Прво одаберите податке и ступац Нормал.
- Идите на картицу Уметање и одаберите раштркани граф.
- Добићемо графикон испод који је приказан на слици испод.
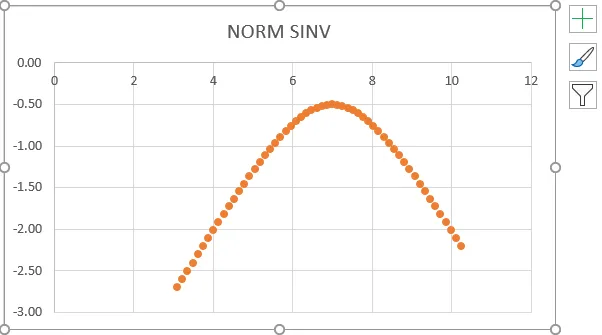
- Из горњег снимка заслона можемо видети да смо добили тачно обрнуту нормалну дистрибуцију која приказује исту вредност вредности приказану доле.

Пример бр. 3 - Подешавање леве и десне кривуље
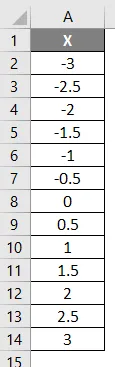
У овом примјеру конфигуришемо лијеву и десну криву користећи нормалну дистрибуцијску функцију. Размотрите доле приказане податке као што је приказано у наставку где к има негативне вредности и повећава се на позитивне вредности.
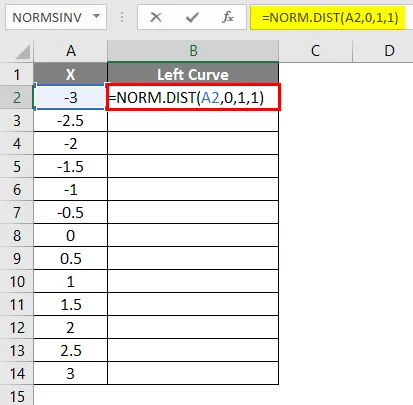
- Примените формулу = НОРМ.ДИСТ (А2, 0, 1, 1).
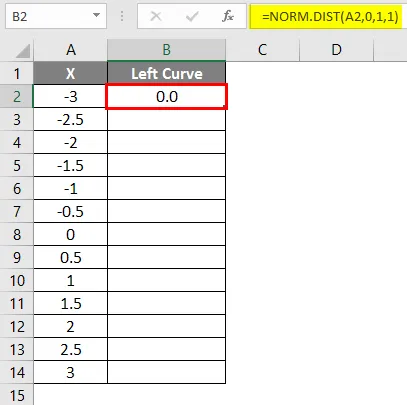
- Након примене формуле резултат је приказан доле.
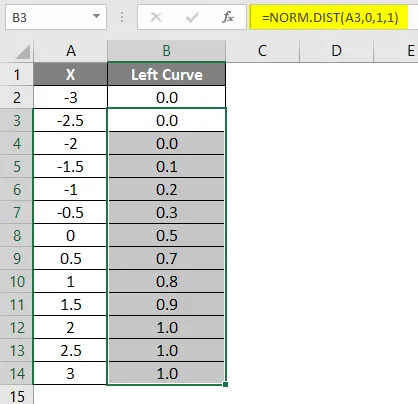
- Превуците формулу у друге ћелије.
- Примените формулу = 1-Б2 .
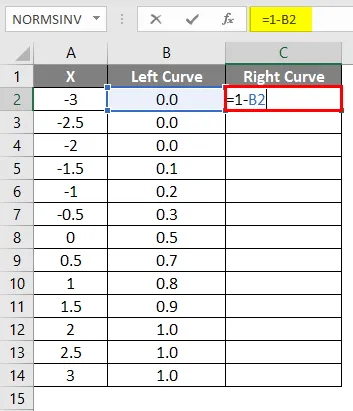
- Након примене формуле резултат је приказан доле.
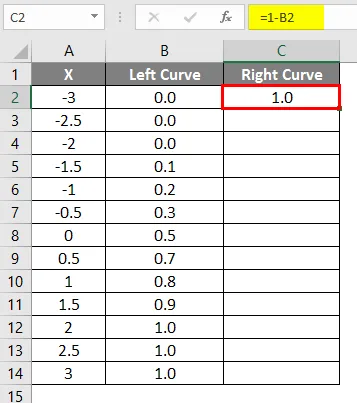
- Превуците исту формулу у остале ћелије.
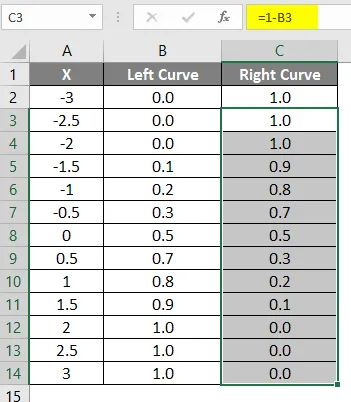
Резултат горе примењене формуле приказан је доле.
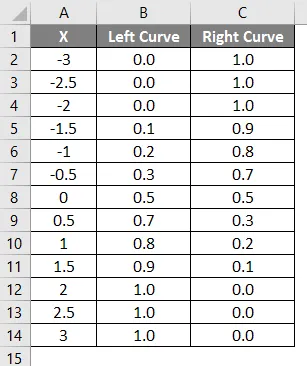
- Вриједности лијеве криве израчунате су примјеном формуле НОРМАЛНА ДИСТРИБУЦИЈА постављањем кумулативне вриједности као Труе и НОРМСИНВ је израчуната кориштењем лијеве кривуље.
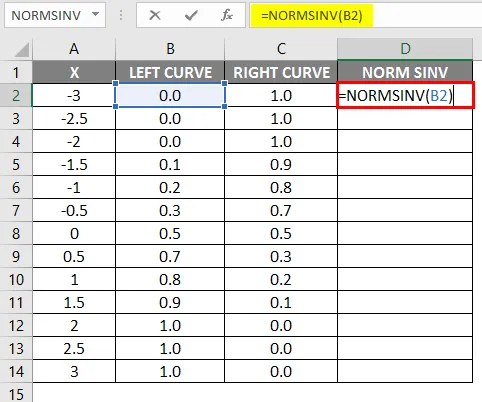
- Након примене формуле резултат је приказан доле.
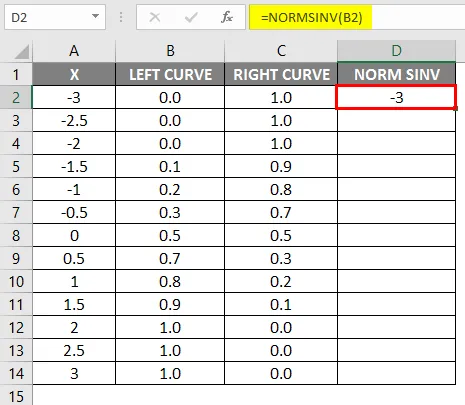
- Превуците исту формулу у остале ћелије.
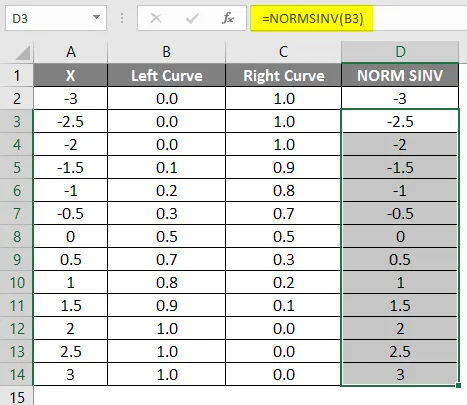
Као што видимо да смо за НОРМСИНВ добили исту вредност која није ништа друго него обрнута нормална дистрибуција. На исти начин добићемо вредност десне криве израчунавањем вредности 1-леве криве. У следећем кораку провераваћемо како ћемо постићи висину к користећи раштркани граф.
- Изаберите леву колону леве и десну криву.
- Идите да убаците мени.
- Изаберите раштркани граф на следећи начин.
Добићемо резултат испод графикона као што је приказано испод.
НОРМ СИНВ Граф:
На доњем графикону можемо видети да лева крива НОРМ ДИСТРИБУЦИЈЕ има тачно подударање за (0, 0, 5) која лежи у средини линије где ћемо добити исти граф ако се пријавимо за НОРМДИСТ.
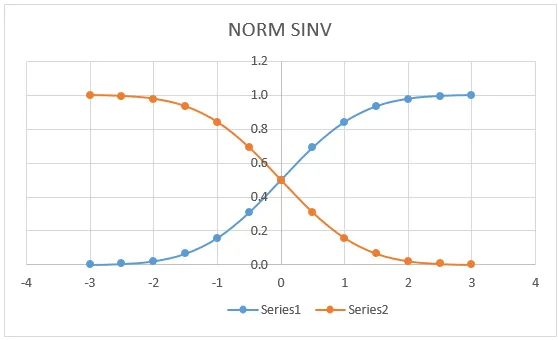
Овде на горњем графу се врло јасно види да смо добили тачну средњу вредност у средишњој тачки која означава:
- Кс = 0
- Лева крива = 0, 5
- Десна крива = 0, 5
Приказали смо га да видимо НОРМСИНВ вредности у графичком формату као што је приказано у наставку.
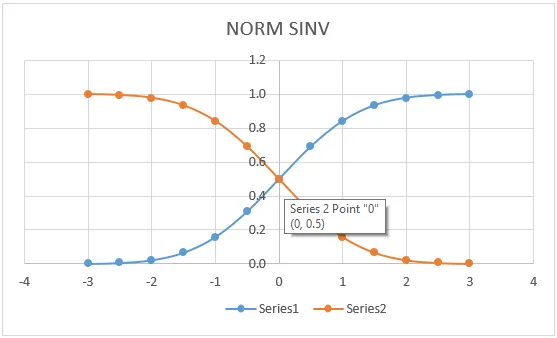
Ствари које треба запамтити о Екцелу НОРМСИНВ
- #валуе! До грешке долази када је дати аргумент не нумеричка или логичка вриједност.
- У функцији нормалне дистрибуције обично добијамо #НУМ! грешка због аргумента стандардног одступања је мања или једнака нули.
Препоручени чланци
Ово је водич за Екцел НОРМСИНВ. Овде смо расправљали о томе како користити НОРМСИНВ у Екцелу заједно са практичним примерима и бесплатним екцел шаблоном. Можете и да прођете кроз друге наше предложене чланке -
- Како се користи поље са именима у Екцелу?
- Рад са Матрик-ом у Екцелу
- Шта ако анализа у Екцелу
- НПВ формула у Екцелу