
Поиссонова формула расподјеле (Садржај)
- Формула
- Примери
- Калкулатор
Шта је Поиссонова формула за дистрибуцију?
У вероватноћи и статистици постоје три врсте дистрибуције засноване на континуираним и дискретним подацима - нормална, биномна и Поиссонова дистрибуција. Нормална дистрибуција је често као Белл кривуља. Поиссонова дистрибуција често се назива и Дистрибуција ретких догађаја. Ово се углавном користи за предвиђање вероватноће да ће се догодити догађаји на основу тога колико се често догађај десио у прошлости. Даје могућност одређеног броја догађаја који се дешавају у одређеном периоду. Користи се у многим стварним ситуацијама.
Формула за проналажење Поиссонове дистрибуције дата је у наставку:
P(x) = (e -λ * λ x) / x!
За к = 0, 1, 2, 3…
Овај експеримент генерално броји број догађаја који су се десили на том подручју, удаљеност или обим. Упоредо са тим, може се наћи Ланац догађаја који није ништа друго него ланац појава истог догађаја током одређеног временског периода. Поиссонова дистрибуција има следеће заједничке карактеристике.
- Догађај се може догодити било који број у било које вријеме.
- Догађај може да размотри све мере као што су количина, површина, удаљеност и време.
- Међутим, вероватноћа да ће се догађај догодити у било којој од горе наведених мера је иста.
- Сваки догађај не зависи од свих осталих догађаја што значи да вероватноћа да се догађај не деси не утиче на друге догађаје који се дешавају истовремено.
Примери формуле расподјеле Поиссона
Узмимо пример како бисмо боље разумели израчунавање Поиссонове дистрибуције.
Можете преузети овај предложак Екцелове формула Поиссонове дистрибуције овде - Поиссонова шаблона за формулу дистрибуције ПоиссонПоиссонова формула расподјеле - Пример бр. 1
Просечан број годишњих незгода које се дешавају на платформи Железничке станице током кретања возова је 7. Да бисте идентификовали вероватноћу да ове године постоје тачно 4 инцидента на истој перону, може се користити Поиссонова формула за дистрибуцију.
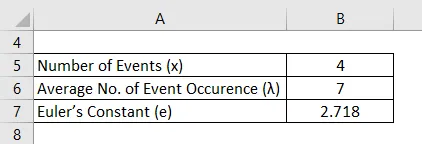
Решење:
Поиссонова расподјела израчунава се према нижој формули
П (к) = (е -λ * λ к) / к!
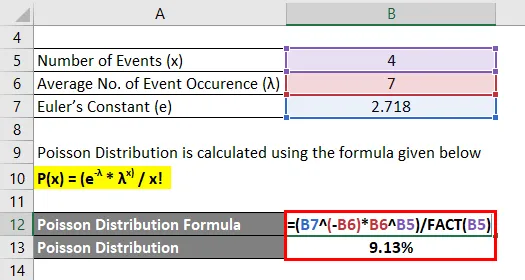
- П (4) = (2.718 -7 * 7 4) / 4!
- П (4) = 9, 13%
За дати пример, постоји 9, 13% шансе да ће се догодити тачно исти број несрећа које се могу догодити ове године.
Поиссонова формула расподјеле - Пример бр. 2
Број грешака при куцању дактилографкиња има Поиссонову дистрибуцију. Грешке се раде независно по просечној стопи од 2 по страници. Пронађите вероватноћу да писмо од три странице не садржи грешке.
Овде је просечна стопа по страници = 2 и просечна стопа за 3 странице (λ) = 6
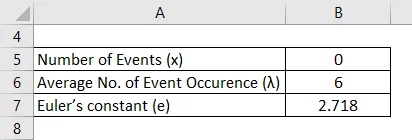
Решење:
Поиссонова расподјела израчунава се према нижој формули
П (к) = (е -λ * λ к) / к!
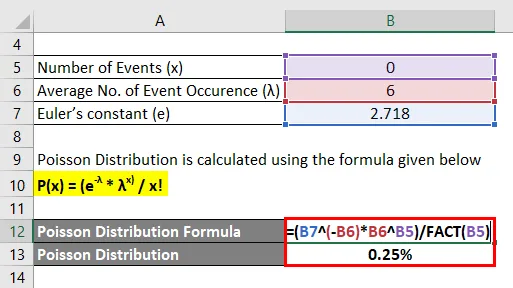
- П (0) = (2.718 -6 * 6 0 ) / 0!
- П (0) = 0, 25%
Отуда постоји 0, 25% шансе да неће бити грешака за 3 странице.
Напомена : к 0 = 1 (било која вредност 0 увек ће бити 1) ; 0! = 1 (нулта фабрика ће увек бити 1)Објашњење
Испод је корак по корак приступ израчунавању Поиссонове формуле дистрибуције.
Корак 1: е је Еулерова константа која је математичка константа. Вредност е-а је 2.718 .
Корак 2: Кс је број стварних догађаја који су се догодили. Може имати вредности попут следећег. к = 0, 1, 2, 3…
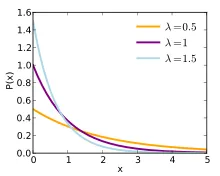
Корак 3: λ је средњи (просечан) број догађаја (познат и као „параметар расподјеле Поиссона“). Ако узмете једноставан пример за израчунавање λ => 1, 2, 3, 4, 5. Ако у горњој формули примените исти скуп података, н = 5, дакле значи = (1 + 2 + 3 + 4 + 5) / 5 = 3. За велики број података ручно проналажење медијане није могуће. Стога је од велике важности користити формулу за велики број скупова података. Овде у прорачуну Поиссонове дистрибуције обично ћемо директно добити просечни број. На основу вредности λ, Поиссонов граф може бити унимодални или бимодални, као ниже.
4. корак: к! је Фактор стварних догађаја који су се догодили к. Испод је пример како израчунати фактороријум за дати број.
Ако узмете једноставан пример за израчунавање Факторорија реалног скупа података => 1, 2, 3, 4, 5.
- Икс! = к * (к-1) * (к-2) * (к-3) * …… 3 * 2 * 1
- 5! = 5 * (5-1) * (5-2) * (5-3) * (5-4)
- 5! = 5 * 4 * 3 * 2 * 1
- 5! = 120
Релевантност и употреба Формуле дистрибуције Поиссона
Поиссонова дистрибуција може радити ако је скуп података дискретна дистрибуција, а свака појава је неовисна о осталим догађајима који се догађају, описује дискретне догађаје у интервалу, догађаји у сваком интервалу могу бити у распону од нуле до бесконачности и значи да број догађаја мора бити константна током целог процеса. Зависно од вриједности параметра (λ), дистрибуција може бити унимодална или бимодална. Поиссонова дистрибуција је дискретна дистрибуција, значи да се догађај може констатовати само да се дешава или не одвија, што значи да се број може навести само у целим бројевима. Фракцијски догађаји догађаја нису део овог модела. Резултати исхода могу се класификовати као успех или неуспех. Ово се широко користи у свету:
- Анализа података за предиктивну анализу података
- Предвиђања берзи
- Предвиђања тржишта продаје
- Предвиђања ланца понуде и потражње
- Лако је доступан на Амазон Веб Сервицес (АВС) платформама
- Преглед и процена покрића пословног осигурања
Остале примјене Поиссонове дистрибуције произлазе из отворенијих проблема. На пример, може се користити за одређивање најмање потребне количине ресурса у позивном центру на основу просечних примљених позива и чекања на чекању. Укратко, списак апликација може се додавати све више и више, јер се користи у практичне светске статистичке сврхе.
Калкулатор расподјеле Поиссонове формуле
Можете користити следећи Поиссон Дистрибутион Цалцулатор
| λ | |
| Икс | |
| П (к) | |
| П (к) = | (е- λ * λ к ) / к! | |
| (0 -0 * 0 0 ) / 0! = | 0 |
Поиссонова формула за дистрибуцију у Екцелу (са Екцеловим предлошком)
Овде ћемо направити још један пример Поиссонове дистрибуције у Екцелу. То је врло лако и једноставно.
Израчунајте Поиссонову дистрибуцију у Екцелу помоћу функције ПОИССОН.ДИСТ.
Испод је синтакса формула Поиссонове дистрибуције у Екцелу.

Поиссонова дистрибуција има следећи аргумент:
Где,
- к = Број појава за које је вероватноћа мора бити позната.
- Средња вредност = Просечан број појава током временског периода.
- Кумулативно = Његова вредност ће бити лажна ако нам треба тачна појава догађаја и Труе ако ће број случајних догађаја бити између 0 и тог догађаја.

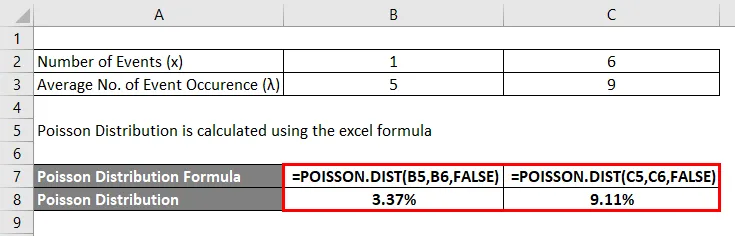
Поиссонова дистрибуција се израчунава помоћу екцел формуле
Препоручени чланци
Ово је водич за Поиссонову формулу дистрибуције. Овде смо расправљали о томе како израчунати Поиссонову расподелу заједно са практичним примерима. Такође нудимо Поиссон-ов Калкулатор дистрибуције са довнлоад-офом екцел предлошка. Такође можете погледати следеће чланке да бисте сазнали више -
- Калкулатор за стандардну нормалну формулу расподјеле
- Прорачун формуле за дистрибуцију Т са предлошком Екцел
- Формула за израчунавање анализе варијанце
- Шта је формула нето вредности имовине?