
Хармонска средња формула (Садржај)
- Хармонска средња формула
- Примери хармоничне средње формуле (са Екцеловим предлошком)
- Хармонични калкулатор средње формуле
Хармонска средња формула
Хармонска средина је у основи врста просека која се користи у статистици која је реципрочна од аритметичке средње вредности реципрочних. Хармонска средина је увек мања од аритметичких средстава истог скупа података. Хармонска средина се обично не користи као аритметичка или геометријска средина и користи се у специфичним ситуацијама или када се ради о просецима јединица, као што су просечна брзина путовања и други омјери. Ово се такође користи у области финансија за израчунавање мултиплета цена попут односа цене и зараде, однос цене и продаје, итд. Разлог за то је ако за израчунавање тих вредности користимо пондерисану аритметичку средину, високе тачке података ће добити већу тежину и ниже тачке података добиће мању тежину што ће створити проблем и неће нам дати прави вишеструки.
Претпоставимо да имамо скуп података са н тачака података и даје их Кс: (Кс1, Кс2, Кс3 …… ..Ксн).
Формула за хармоничну средину је
Harmonic Mean = n / (1/X1 + 1/X2 + 1/X3 ………… 1/Xn)
Где:
- Кс1, Кс2, … Ксн - Точке података
- н - Укупан број података
Кораци за израчунавање хармонске средње вредности:
- Узмите реципрочно све тачке података у скупу података.
- Након тога пронађите средњу / просјечну вриједност тих вриједности.
- Следећи и последњи корак је узимање реципрочне вредности да би се дошло до хармоничне средње вредности.
Примери хармоничне средње формуле (са Екцеловим предлошком)
Узмимо пример како бисмо боље разумели израчунавање хармонске средње вредности.
Можете преузети овај Хармонски средњи образац овде - Хармонични средњи предложакХармонска средња формула - Пример бр. 1
Рецимо да имате скуп података са 10 тачака података и за то желимо израчунати хармоничну средину.
Скуп података: (4, 6, 8, 9, 22, 83, 98, 45, 87, 10)
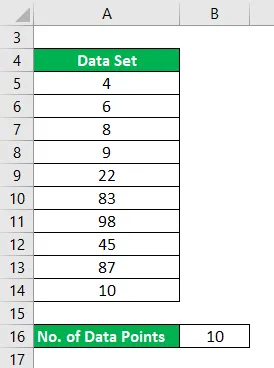
Реципрочно ће се израчунати као:
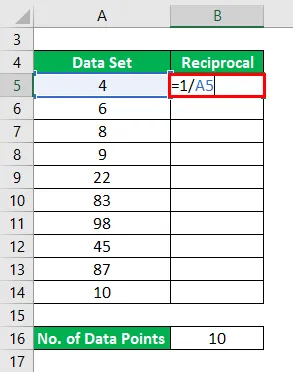
Резултат ће бити наведен у наставку.
Слично томе, морамо израчунати узајамно за све тачке података.
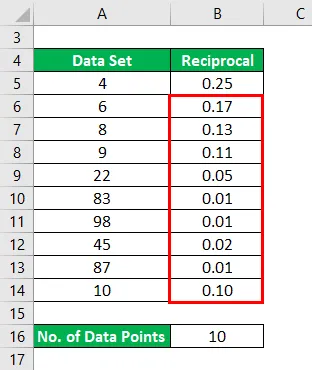
Средња вредност реципрочног израчунава се као
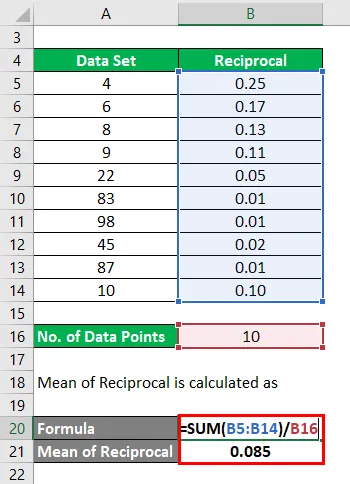
- Средња вредност реципрочног = (0, 25 + 0, 17 + 0, 13 + 0, 11 + 0, 05 + 0, 01 + 0, 01 + 0, 02 + 0, 01 + 0, 10) / 10
- Средња вредност реципрочног = 0, 85 / 10
- Средња вредност реципрочног = 0, 085
Хармонска средња вредност израчунава се помоћу доле наведене формуле
Хармонска средња = н / (1 / Кс1 + 1 / Кс2 + 1 / Кс3 ………… 1 / Ксн)
Хармонска средња вредност = 1 / средња вредност реципрочног
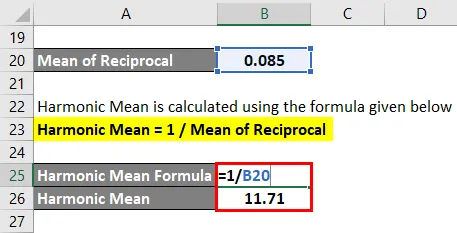
- Хармонска средња вредност = 1 / 0, 085
- Хармонска средња вредност = 11, 71
Хармонска средња формула - Пример бр. 2
Сада погледајте неке друге примере из практичног живота да бисте јасније схватили значење и увидели разлику између аритметичке и хармоничне средње вредности.
Рецимо да возите аутомобил и путујете у неки други град. Укупно време за ваше путовање је 4 сата, од чега возите брзином од 60 км / час током првог сата, 50 км / сат током другог сата, 100 км / час током трећег сата и 40 км / сат током 4. сат.
Дакле, ваша просечна брзина се може израчунати простом средњом:
- Просечна брзина = (60 + 50 + 100 + 40) / 4
- Просечна брзина = 250/4
- Просечна брзина = 62, 5 км / сат
Али рецимо да је податак да сте током прве половине времена возили брзином од 55, 5 км / час, а следећу половину брзином од 70 км / час. У том случају морамо користити хармоничну средину да бисмо пронашли просечну брзину.
Хармонска средња вредност израчунава се помоћу доле наведене формуле
Хармонска средња = н / (1 / Кс1 + 1 / Кс2 + 1 / Кс3 ………… 1 / Ксн)
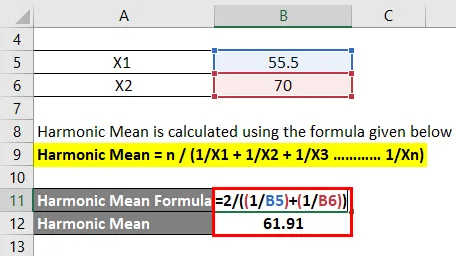
- Хармонска средња вредност = 2 / ((1 / 55.5) + (1/70))
- Хармонска средња вредност = 61, 91 км / сат
Ако видите овде, вредност хармоничне средње вредности је мања од простог просека.
Објашњење
Иако се хармоничка средина у основи користи за проналажење просека скупа података, попут једноставне аритметичке средње вредности, она се не израчунава као једноставно аритметичка средина. Ако имамо велики скуп података, израчунавање хармонске средње вредности постаће сложено и дуготрајно. Са сложеношћу долази до забуне и шансе за грешку. Стога треба бити врло опрезан док израчунавамо хармоничну средину великог скупа података. Пошто узимамо реципрочно у прорачуну хармоничке средње вредности, највећа тежина се даје најнижој вредности и обрнуто. Понекад то није потребно.
Други недостатак је да ако је било која од података у скупу података једнака 0, хармонска средња вриједност не може се израчунати с обзиром да к / 0 није дефинирано. На неки начин, хармонична средина има врло ограничен домет за разлику од аритметичке средње. Такође, ово је изузетно осетљиво на одметнике и екстремне вредности.
Релевантност и употреба хармонске средње формуле
Видели смо вишеструка ограничења хармонијске средине и то је разлог што нема много практичне примене. Али постоје и неке користи и позитивне поене. Хармонска средина је строго дефинисана и због тога је погодна за даље математичке операције. Такође, за разлику од геометријске средње вредности, на то не утичу флуктуације узорковања. Будући да даје малу тежину малим скуповима података, што је понекад пожељно да подаци не буду пристрани према високим вредностима. Ситуације које укључују време и стопе, хармонична средина дају боље и прецизније резултате од једноставне средње вредности.
Све што је речено и учињено, хармонична средина има неколико предности, али с обзиром да има ограничен опсег, а недостаци су му већи, не користи се често и има ограничено присуство.
Хармонични калкулатор средње формуле
Можете користити следећи Хармонични средњи калкулатор
| н | |
| Кс1 | |
| Кс2 | |
| Кс3 | |
| Хармонска средња формула | |
| Хармонска средња формула = |
|
|
Препоручени чланци
Ово је водич за средње хармоничну формулу. Овде смо расправљали о томе како израчунати хармоничну средину заједно са практичним примерима. Такође нудимо Хармониц Средњи калкулатор са довнлоад-ом Екцел шаблона. Такође можете погледати следеће чланке да бисте сазнали више -
- Водич за распон формуле
- Најбољи примјери формуле времена за удвостручавање
- Калкулатор за формулу потонућег фонда
- Како израчунати ДПМО?