
Маргин оф Еррор Формула (Садржај)
- Формула грешке
- Примери маргине формуле грешке (са Екцеловим предлошком)
- Маргин оф Еррор Формула Цалцулатор
Формула грешке
У статистици, израчунавамо интервал поузданости да видимо где ће вредност података статистичких узорака пасти. Распон вредности које су испод и изнад узорка статистике у интервалу поузданости познат је као маргина грешке. Другим речима, у основи је степен грешке у узорку статистике. Што је већа грешка, мање ће бити поверења у резултате, јер је степен одступања у овим резултатима врло висок. Као што му име каже, грешка је распон вриједности изнад и испод стварних резултата. На пример, ако добијемо одговор у анкети у којој је 70% људи одговорило „добро“, а грешка је 5%, то значи да генерално 65% до 75% популације мисли да је одговор „добар“ .
Формула за грешку -
Margin of Error = Z * S / √n
Где:
- З - З резултат
- С - Стандардно одступање становништва
- н - Величина узорка
Друга формула за израчунавање грешке је:
Margin of Error = Z * √((p * (1 – p)) / n)
Где:
- п - узорак пропорција (део узорка који је успешан)
Да бисте пронашли жељени з резултат, морате да знате интервал поузданости узорка, јер З оцена зависи од тога. Испод је дата табела да бисте видели однос интервала поверења и з оцене:
| Интервал поверења | З - Резултат |
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
Једном када знате интервал поузданости, можете користити одговарајућу з вредност и одатле израчунати границу грешке.
Примери маргине формуле грешке (са Екцеловим предлошком)
Узмимо пример како бисмо боље разумели израчунавање маргине грешке.
Овдје можете преузети овај шаблон Маргин оф Еррор - Маргин оф Еррор ТемплатеФормула грешке - Пример бр. 1
Рецимо да проводимо анкету да видимо каква је оцена која добијају студенти. Насумично смо одабрали 500 ученика и питали их за оцену. Просјек тога је 2, 4 од 4, а стандардно одступање је 30%. Претпоставимо да је интервал поузданости 99%. Израчунајте грешку.
Решење:
Маргин оф Еррор израчунава се помоћу доленаведене формуле
Маргина грешке = З * С / √н
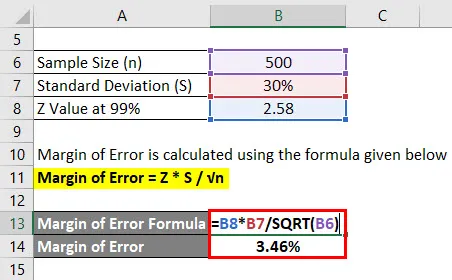
- Маргин оф еррор = 2, 58 * 30% / √ (500)
- Маргина грешке = 3, 46%
То значи да је са 99% самопоуздања просечна оцена студената 2, 4 плус или минус 3, 46%.
Маргина грешке формуле - пример бр. 2
Рецимо да лансирате нови здравствени производ на тржиште, али збуњени сте који ће укус вољети људе. Збуњени сте између ароме банане и ванилије и одлучили сте да спроведете анкету. Ваша популација за то је 500.000 што је ваше циљно тржиште и ван тога сте одлучили да питате мишљење 1000 људи и то ће бити узорак. Претпоставимо да је интервал поузданости 90%. Израчунајте грешку.
Решење:
Једном када је истраживање обављено, сазнали сте да се 470 људи свидело укусу банане, а 530 је затражило арому ванилије.
Маргин оф Еррор израчунава се користећи ниже формулу
Маргин оф Еррор = З * √ ((п * (1 - п)) / н)
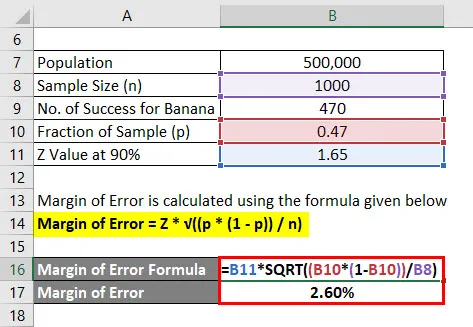
- Маргин оф Еррор = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Маргина грешке = 2, 60%
Дакле, са 90% поузданости можемо рећи да је 47% свих људи волело укус банане плус или минус 2.60%.
Објашњење
Као што је горе речено, грешка нам помаже да схватимо да ли је величина узорка вашег истраживања одговарајућа или не. У случају да је грешка марже превелика, може се догодити да је наша величина узорка премала и да то морамо повећати тако да се резултати узорка поклапају са резултатима популације.
Постоје неки сценарији у којима грешка неће бити од велике користи и неће нам помоћи у праћењу грешке:
- Ако питања анкете нису осмишљена и не помажу у тражењу одговора
- Ако људи који реагују на анкету имају пристраности у вези с производом за који се врши анкета, онда резултат не треба бити баш тачан
- Ако је узорак који је сам изабран прави представник популације, у том случају ће и резултати бити на претек.
Такође, једна велика претпоставка је да је становништво нормално расподељено. Дакле, ако је величина узорка премала и дистрибуција становништва није нормална, з оцена се не може израчунати и нећемо моћи наћи маргину грешке.
Релевантност и употреба формуле грешке
Кад год користимо узорке података да пронађемо неки релевантан одговор за скуп становништва, постоји одређена несигурност и шансе да резултат може одступати од стварног резултата. Граница грешке ће нам рећи да који је ниво одступања постоји излазност узорка. Морамо смањити границу грешке тако да резултати узорака приказују стварну причу о подацима становништва. Дакле, нижа је грешка и бољи ће бити резултати. Граница грешке допуњава и употпуњава статистичке информације које имамо. На пример, ако се анкетом утврди да 48% људи радије проводи време код куће током викенда, не можемо бити тако прецизни и у тим подацима постоје неки елементи који недостају. Када смо овде увели маргину грешке, рецимо, 5%, тада ће се исход тумачити као да је 43-53% људи волело идеју да буду код куће током викенда, што има потпуно смисла.
Маргин оф Еррор Формула Цалцулатор
Можете да користите следећу маржу грешке Калкулатор
| З | |
| С | |
| √н | |
| Маргина грешке | |
| Маргина грешке | = |
|
|
Препоручени чланци
Ово је водич за формулу Маргин оф Еррор. Овде смо разговарали о томе како израчунати маржу грешке заједно са практичним примерима. Пружамо и калкулатор Маргин оф Еррор („грешка марже“) са софтвером за скидање Екцеловог предлошка. Такође можете погледати следеће чланке да бисте сазнали више -
- Водич за форму амортизације правих линија
- Примери формуле времена удвостручења
- Како израчунати амортизацију?
- Формула за теорем централне границе
- Алтман З Сцоре | Дефиниција | Примери
- Формула амортизације | Примери са Екцел предложаком