
Увод у сортирање алгоритама у ЈаваСцрипт-у
Слично као у већини других програмских језика, можете наићи на сценарије у којима морате неке врсте бројева у ЈаваСцрипту сортирати узлазним или силазним редоследом. Да бисмо то постигли, можемо користити многе алгоритме као што су Буббле сорт, Сорт Сорт, сортирање, Куицксорт, итд. Ови алгоритми се не само разликују у начину функционисања, већ имају и различите захтеве у погледу меморије и времена, копајте дубље у неке од важних алгоритама за сортирање и погледајте како их можете користити у свом ЈаваСцрипт коду.
Топ 6 сортирања алгоритама у ЈаваСцрипт-у
Ево неколико алгоритама за разврставање у ЈаваСцрипт-у који су објашњени у наставку са примерима:
1. Алгоритам Буббле Сорт
Сматрана једним од најчешћих алата ове трговине, Буббле сортирање ради стварајући петљу која сваку ставку у низу упоређује са другом ставком. Ако је упоређени предмет мањи од оног на руци, заменимо њихова места. То траје све док не добијемо пролаз гдје ниједна ставка у низу није већа од ставке која се налази поред ње.
Буббле Сорт има О (н 2 ) временску сложеност и О (н) сложеност простора.
Шифра:
function swap(arr, firstIndex, secondIndex)(
var temp = arr(firstIndex);
arr(firstIndex) = arr(secondIndex);
arr(secondIndex) = temp;
)
function bubbleSortAlgo(arraaytest)(
var len = arraaytest.length,
i, j, stop;
for (i=0; i < len; i++)(
for (j=0, stop=len-i; j < stop; j++)(
if (arraaytest(j) > arraaytest(j+1))(
swap(arraaytest, j, j+1);
)
)
)return arraaytest;
)
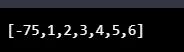
console.log(bubbleSortAlgo((3, 6, 2, 5, -75, 4, 1)));
Излаз:
2. Алгоритам избора сортирања
Сада када смо завршили са расправом о алгоритму сортирања буббле, погледајмо само као популаран алгоритам за сортирање назван Селецтион Сорт.
За разлику од Буббле Сорт, ми се фокусирамо на проналажење најмање вредности у низу да бисмо завршили сортирање. Ево корак по корак рашчлањивање начина функционисања Сорт Селецтион:
- Претпостављамо да је прва ставка у низу најмања.
- Упоређујемо ову ставку са следећом ставком у низу.
- Ако је сљедећа ставка мања од оне која је при руци, сљедећу ставку постављамо као нову најмању вриједност.
- Настављамо понављати ове кораке док не дођемо до краја низа.
- Када пронађемо вредност у низу која је мања од оне са којом смо започели, мењамо њихове позиције.
- Настављамо са упоређивањем и прелазимо на следећу ставку. Док се целокупни низ не сортира.
Баш као алгоритам Буббле Сорт, сорта Селецтион има О (н 2 ) временску сложеност и О (н) сложеност простора.
Шифра:
function SelectionSortAlgo(array, compare_Function) (
function comp(a, b) (
return a - b;
)
var min = 0;
var index = 0;
var temp = 0;
compare_Function = compare_Function || compare;
for (var i = 0; i < array.length; i += 1) (
index = i;
min = array(i);
for (var j = i + 1; j < array.length; j += 1) (
if (compare_Function(min, array(j)) > 0) (
min = array(j);
index = j;
)
)
temp = array(i);
array(i) = min;
array(index) = temp;
)
return array;
)
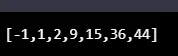
console.log(SelectionSortAlgo((9, 15, 2, 44, -1, 36, 1), function(a, b) ( return a - b; )));
Излаз:
3. Спајање Алгоритам сортирања
Слично сортирању и избору Буббле Сорт, сортирање спајања је један од популарних алгоритама за сортирање у рачунарској науци, можете га имплементирати у већини програмских језика и има добре перформансе без да су сувише потребни ресурси.
Мерге Сорт користи методу Дивиде анд цонкуер за сортирање низа или било које листе елемената. Израз дијели и осваја значи да један велики проблем дијелимо на неколико мањих проблема, а затим рјешавамо те мале проблеме. Једном када се реше мањи проблеми, комбинујемо резултате који резултирају решавањем великог проблема.
Разумевање алгоритма је заправо једноставно:
- Дељени низ подијелимо на н поља, а сваки од ових низова садржи само 1 елемент.
- Спајање низова да бисте произвели нови низ.
- Понављајте корак 2 док не остане само један низ који ће бити сортирани низ.
Шифра:
function merge_sort_algo(left, right)
(
var i = 0;
var j = 0;
var result = ();
while (i < left.length || j < right.length) (
if (i === left.length) (
// j is the only index left_part
result.push(right(j));
j++;
)
else if (j === right.length || left(i) <= right(j)) (
result.push(left(i));
i++;
) else (
result.push(right(j));
j++;
)
)
return result;
)
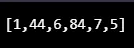
console.log(merge_sort_algo((1, 44, 6), (84, 7, 5)));
Излаз:
4. Алгоритам за брзо сортирање
Куицксорт је један од најефикаснијих начина сортирања елемената у рачунарским системима. Симилор за спајање сорте, Куицксорт ради на алгоритму за поделу и освајање. У овом случају у низу проналазимо осовину за поређење са свим другим низовима елемената са, а затим премештамо ставке на начин да су све ставке испред наших одабраних стожерних ставки мање и да су све ставке после стопе стожера веће у величини. Једном када то учинимо, кључ је у томе да то стално понављамо и имаћемо свој сортирани низ.
Следе кораци који се могу применити у имплементацији алгоритма за брзо постизање:
- Одаберемо елемент матрице и зовемо га „Пивот Поинт“
- Покрећемо показивач који се зове леви показивач и из којег се налази први елемент у низу.
- Слично томе, покрећемо показивач који се зове десни показивач на последњој ставци низа.
- Ако је вредност елемента на левом показивачу мања у поређењу са одабраном тачком окрета, померимо леви показивач лево (додајте +1) и настављамо понављати све док вредност на левом показивачу не буде већа од вредност тачке тачке вешања или једнака истој.
- Ако је вредност елемента на десном показивачу на листи већа од вредности елемента који се окреће, ми померимо десни показивач улево. Понављајте ово све док вредност са десног бочног показивача не буде нижа (или једнака) вредности стопе.
- Када је вредност левог показивача мања или једнака вредности десног показивача, замените вредности.
- Померите десни показивач лево од једног, леви кажипрст десно по један.
- Понављајте док се леви и десни показивачи не сусретну.
Шифра:
function quickSortAlgo(origArray) (
if (origArray.length <= 1) (
return origArray;
) else (
var left = ();
var right = ();
var newArray = ();
var pivot = origArray.pop();
var length = origArray.length;
for (var i = 0; i < length; i++) (
if (origArray(i) <= pivot) (
left.push(origArray(i));
) else (
right.push(origArray(i));
)
)
return newArray.concat(quickSortAlgo(left), pivot, quickSortAlgo(right));
)
)
var myArray = (13, 50, 2, 45, -1, 74, 11 );
var arreySorted = quickSortAlgo(myArray);
console.log(arreySorted);
Излаз:
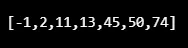
5. Алгоритам сортирања уметања
Када је у питању једноставна имплементација, врста уметања је опште позната као један од једноставнијих алгоритама. У Постави уметања, елементи матрице се упоређују једни с другима и затим сређују у одређеном редоследу. Ово је веома слично уређивању карата у палуби. Врста уметања имена долази из процеса одабира елемента и његовог уметања на његово исправно место, а затим понављања за све елементе.
Ево како алгоритам ради:
- Први елемент матрице сматра се већ сортираним.
- Изаберите следећи елемент матрице.
- Упоредите одабрани елемент са свим елементима у низу.
- Померите сваки елемент у низу који је већи од вредности изабраног елемента.
- Уметните елемент
- Понављајте кораке 2 до 5 док се низ не сортира.
Шифра:
function insertion_Sort_algo(arr)
(
for (var i = 1; i < arr.length; i++)
(
if (arr(i) < arr(0))
(
arr.unshift(arr.splice(i, 1)(0));
)
else if (arr(i) > arr(i-1))
(
continue;
)
else (
for (var j = 1; j < i; j++) (
if (arr(i) > arr(j-1) && arr(i) < arr(j))
(
arr.splice(j, 0, arr.splice(i, 1)(0));
)
)
)
)
return arr;
)
console.log(insertion_Sort_algo((44, 20, 26, 54, -9, 41, 16)));
Излаз:
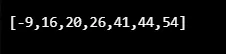
6. Алгоритам хеоп сортирања
Сортирање хеапом је начин сортирања елемената користећи структуру података „Хеап“. Метода је прилично слична техници селекције, о којој смо разговарали раније. Сада се можда питате о Хеапс-у и како су они дефинисани, пре него што пређемо на алгоритам, прво да разумемо хрпе.
Укратко, гомила је бинарно дрво са неким додатним правилима. Једно правило каже да у хрпи, дрво мора бити комплетно бинарно стабло што једноставно значи да је потребно попунити све чворове на тренутном нивоу пре додавања још једног. Следеће правило за гомилу је да мора постојати дефинисан однос детета и родитеља са вредностима елемената гомиле.
У минутрини, вредност родитеља мора бити мања од деце. Као што можете погодити, у највећој гомили родитеља вредност мора бити већа од детета.
Сада када су дефиниције изостане, погледајмо како функционише гомила:
- Прво стварамо максимум хеап који осигурава да се елемент највише вредности налази на врху.
- Пребацујемо горњи елемент са последњим елементом из хрпе и уклањамо горњи елемент из хрпе и чувамо га у сортираном низу.
- Стално понављамо први и други корак док у хрпи не остане само један елемент.
Једна ствар коју треба имати на уму је да Хеапс није изворно подржан у ЈаваСцрипту, па морамо посезати за имплементацијом Хеапса помоћу низова. Свемирска сложеност сортирања хем је О (1) која је одлична, а иако је мало сложенија у односу на сортирање или уметање сортирања када је у питању разумевање и примена, мислим да су предности перформанси то је на крају боље искористити у велики пројекти.
Шифра:
var arrLength;
function heapRoot(input, i) (
var left = 2 * i + 1;
var right = 2 * i + 2;
var max = i;
if (left input(max)) (
max = left;
)
if (right input(max)) (
max = right;
)
if (max != i) (
swap(input, i, max);
heapRoot(input, max);
)
)
function swap(input, index_A, index_B) (
var temp = input(index_A);
input(index_A) = input(index_B);
input(index_B) = temp;
)
function heapSortAlgo(input) (
arrLength = input.length;
for (var i = Math.floor(arrLength / 2); i >= 0; i -= 1) (
heapRoot(input, i);
)
for (i = input.length - 1; i > 0; i--) (
swap(input, 0, i);
arrLength--;
heapRoot(input, 0);
)
)
var arr = (12, 10, 22, 55, -8, 64, 14);
heapSortAlgo(arr);
console.log(arr);
Излаз:
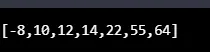
Закључак
Поредавање је важан део креирања апликација и веб локација са ЈаваСцрипт-ом. Сада када сте упознати са неким од најважнијих алгоритама да бисте обавили посао, требало би да се осећате самоувереније у ЈС Девелопмент.
Једна важна чињеница коју треба имати на уму о разним сортирањима је да заиста не морате превише да се оптерећујете алгоритмом који ћете користити у већини случајева. Сада када је рачунарски хардвер толико моћан, модерни процесори за телефон и Десктоп неће покварити никакав зној у сортирању чак стотина елемената у неколико милисекунди. То су само случајеви у којима сте заглавили са спорим хардвером или ситуацијама у којима оптимизујете сваки одељак кода где промена алгоритама за сортирање може бити корисна.
Препоручени чланци
Ово је водич за сортирање алгоритама у ЈаваСцрипт-у. Овде смо расправљали о првих 6 алгоритама за сортирање у ЈаваСцрипт-у, заједно са примерима и имплементацијом кода. Такође можете погледати следеће чланке да бисте сазнали више -
- Компајлери ЈаваСцрипт
- Преокренути у ЈаваСцрипт-у
- Увод у ЈаваСцрипт
- Квадрати у Јави
- Брзо сортирање алгоритама на Јави
- Низови у структури података
- Ц ++ алгоритам | Примери алгоритма Ц ++