
Увод у стандардне примере одступања
Постоји довољно примера стандардних одступања. Стандардна девијација је мјера раширености скупа података, тј. Како су распоређени бројеви. Корисно је за поређење различитих скупова података који могу имати исту средину, али различит распон. Следећи различити пример стандардног одступања даје разумевање о најчешћим врстама ситуација где се стандардно одступање израчунава и како се може израчунати исто
Примери стандардног одступања
Испод су примери стандардног одступања
Стандардно одступање - пример бр. 1
Акције Компаније З продају за 50 долара по акцији и исте понуде следеће исплате за следећу годину:
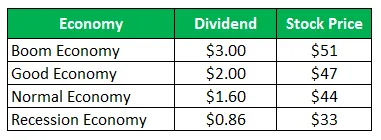
Израчунајте Стандардно одступање када су сва четири сценарија дата подједнако вероватна.
Решење:
Калкулације поврата периода задржавања (ХПР) су следеће -
Формула ХПР
ХПР = ((крај периода вредности - изворна вредност) + приход) / првотна вредност) * 100
За економију бума
- ХПР (бум) = ((51-50) + 3) / 50 = 8, 00%
- ХПР (добро) = ((47-50) + 2) / 50 = -2, 00%
- ХПР (нормално) = ((44-50) + 1, 60) / 50 = -8, 80%
- ХПР (рецесија) = ((33-50) + 0, 86) / 50 = -32, 28%
Прорачун очекиваног поврата
Пошто су сви сценарији подједнако вероватни, вероватноћа свих ће бити ¼
Формула очекиваног повратка
Очекивани повратак = (вероватноћа бума * повратак из бума) + (вероватноћа добра * повратак из добра) + (вероватноћа нормалног * повратак из нормалног) + (вероватноћа рецесије * повратак из рецесије)
- Очекивани поврат = (1/4 к 8%) + (1/4 к -2%) + (1/4 к -8.80%) + (1/4 к -32.28%)
- Очекивани поврат = -8, 77%
Прорачун стандардног одступања
Формула варијације
Варијанца = (вероватноћа бума * (повратак из гума - укупан очекивани повратак) 2) + (вероватноћа добра * (повратак из добра - укупан очекивани повратак) 2) + (вероватноћа нормалног * (повратак из нормалног - укупан очекивани повратак)) 2 ) + (вероватноћа рецесије * (повратак из рецесије –укупни очекивани повратак) 2)
- Варијанца = 1/4 (8 - (-8.77)) 2 + 1/4 (-2 - (-8.77)) 2 + 1/4 (-8.80 - (-8.77)) 2 + 1/4 (-32.28 - (-8.77)) 2
- Варијанца = 219, 95
Формула стандардног одступања
Стандардно одступање биће квадратни коријен варијанце
Стандардно одступање = √ Варијанта
- Стандардно одступање = 219, 95 √
- Стандардно одступање = 14, 83%
Пример стандардног одступања - 2
Стандардна девијација у случају две компаније из портфеља
Уобичајена акција компаније А продаје се за 28 долара по акцији и исте понуде након исплате за следећу годину

Уобичајена акција Компаније Б продаје се за 93 УСД по акцији и исте понуде следећих исплата за следећу годину:

(а) Израчунајте стандардну девијацију компаније А
(б) Израчунајте стандардну девијацију компаније Б
(ц) Израчунајте стандардно одступање портфеља ако је половина инвестиције предузеће А, а половина половина компаније Б
Решење:
За компанију А
Калкулације поврата периода задржавања (ХПР)
Формула ХПР
ХПР = ((крај периода вредности - изворна вредност) + приход) / првотна вредност) * 100
- ХПР (бум) = ((20-28) + 1) / 28 = -25, 00%
- ХПР (нормално) = ((30-28) + 1, 50 / 28 = 12, 50%
- ХПР (рецесија) = ((38-28) + 5) / 28 = 53, 57%
Прорачун очекиваног поврата компаније А
Формула очекиваног повратка
Очекивани повратак = (вероватноћа бума * повратак из бума) + (вероватноћа нормалног * повратак из нормалног) + (вероватноћа рецесије * повратак из рецесије)
- Очекивани поврат = (0, 45 к -25, 00%) + (0, 35 к 12, 50%) + (0, 20 к 53, 57%)
- Очекивани поврат = 3, 84%
Прорачун компаније Стандард Девиатион А
Формула варијације
Варијанца = (Вероватноћа бума * (Повратак из грма - Укупни очекивани повратак) 2) + (Вероватноћа нормалног * (Повратак из нормалног - Укупан очекивани повратак) 2 ) + (Вероватноћа рецесије * (Повратак из рецесије - Укупан очекивани повратак)) 2)
- Варијанца = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Варијанта = 895.15
Формула стандардног одступања
Стандардно одступање биће квадратни коријен варијанце
Стандардно одступање = √ Варијанта
- Стандардно одступање = 95 895.15
- Стандардно одступање = 29, 92%
За компанију Б
Калкулације поврата периода задржавања (ХПР)
Формула ХПР
ХПР = ((крај периода вредности - изворна вредност) + приход) / првотна вредност) * 100
ХПР (бум) = ((200-93) +7) / 93 = 122, 58%
ХПР (нормално) = ((105-93) + 5, 50 / 93 = 18, 82%
ХПР (рецесија) = ((4-93) +2) / 93 = -93, 55%
Прорачун очекиваног поврата
Формула очекиваног повратка
Очекивани повратак = (вероватноћа бума * повратак из бума) + (вероватноћа нормалног * повратак из нормалног) + (вероватноћа рецесије * повратак из рецесије)
- Очекивани поврат = (0, 45к 122, 58%) + (0, 35 к 18, 82%) + (0, 20 к -93, 55%)
- Очекивани поврат = 43, 04%
Прорачун стандардног одступања
Формула варијације
Варијанца = (Вероватноћа бума * (Повратак из грма - Укупни очекивани повратак) 2) + (Вероватноћа нормалног * (Повратак из нормалног - Укупан очекивани повратак) 2 ) + (Вероватноћа рецесије * (Повратак из рецесије - Укупан очекивани повратак)) 2)
- Варијанца = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Варијанта = 6783.65
Формула стандардног одступања
Стандардно одступање биће квадратни коријен варијанце
Стандардно одступање = √ Варијанта
- Стандардно одступање = 836783.65
- Стандардно одступање = 82, 36%
Прорачун очекиваног поврата и стандардног одступања половине портфеља уложене у компанију А и половину у компанију Б.
Стандардно одступање компаније А = 29, 92%
Стандардно одступање компаније Б = 82, 36%
Тежина компаније А = 0, 50
Тежина компаније Б = 0, 50
Формула стандардног одступања портфеља
Стандардно одступање портфеља = (Тежина компаније А * Очекивани повраћај компаније А) + ((Тежина компаније Б * Очекивани повраћај компаније Б)
- Стандардно одступање портфеља = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Стандардно одступање портфеља = 56, 14%
Анализа
Стандардно одступање портфеља је ниже него за појединачно било које акције, јер су залихе разнолике у различитим залихама. Диверзификација доводи до смањења ризика уколико не постоји савршена корелација између приноса на портфељне инвестиције.
Закључак - Стандардни примери одступања
Стандардна девијација мери дисперзију скупа података која је релативна у односу на средњу вредност. Израчунава се као квадратни корен варијанце. Што је већа стандардна девијација хартије од вредности, већа ће бити одступање између сваке цене и просечне вредности, што показује да је распон цена велики. Горе наведени примери су неки од примера Стандардне девијације на различите начине. Постоје и разни други примери који показују да се стандардно одступање може израчунати користећи друге податке.
Препоручени чланци
Ово је водич за стандардне примере одступања. Овде смо расправљали о разним примерима стандардног одступања заједно са детаљним објашњењем . Можда ћете такође погледати следеће чланке да бисте сазнали више -
- Пример фиксних трошкова
- Пример променљивог трошка
- Квантитативни пример истраживања
- Примери монополистичке конкуренције