
Узорак стандардне формуле одступања (садржај)
- Формула
- Примери
Узорак стандардне формуле одступања
У статистици је стандардно одступање у основи мера за проналажење раширености задатих вредности података од средње вредности скупа података. Он мери удаљеност те тачке података и средњу вредност. Што је стандардно одступање веће, то ће бити већа дисперзија и тачке података ће бити далеко од средње вредности. Слично томе, нижа стандардна девијација значи да ће тачке података бити ближе средњој. Врло је корисно у поређењу скупова података који могу имати исту средњу вриједност, али различит распон.
Обично се израчунава стандардно одступање података о популацији, али понекад су подаци о популацији толико огромни да за то није могуће пронаћи стандардно одступање. У том случају се израчунава стандардна девијација узорка која ће постати представник стандардне девијације становништва. Стога ћемо претпоставити да је узорак тачан приказ популације и фокусират ћемо се на стандардну девијацију узорка у овом чланку.
Претпоставимо да имате скуп података Кс са тачкама података (Кс1, Кс2 …… ..Ксн).
Формула за стандардно одступање становништва је дата:
Population Standard Deviation = √ (Σ (X i – X m ) 2 / n )
У случају да вам није дата целокупна популација и имате само узорак (рецимо да је Кс скуп узорка података становништва), тада формула за стандардно одступање узорка даје:
Sample Standard Deviation = √ (Σ (X i – X m ) 2 / (n – 1))
Где:
- Кс и - и вредност скупа података
- Кс м - средња вредност скупа података
- н - Укупан број података
Формула у почетку може изгледати збуњујуће, али на томе је заиста радити. Следе кораци за израчунавање стандардног одступања узорка:
- Пронађите број тачака у скупу података тј. Н
- Затим је следећи корак проналажење средње вредности узорка. То је у основи просек свих вредности.
- Након тога, за сваку тачку података, пронађите разлику те вриједности од средње, а затим је уврстите у квадрат.
- Узмите све вредности у горњем кораку и поделите са н-1.
- Последњи корак је узимање квадратног корена горе израчунатог броја.
Постоји још један начин израчунавања популације и стандардне девијације једноставним коришћењем СТДЕВ.П () функције за стандардно одступање популације и СТДЕВ.С () функције за стандардно одступање узорка у екцелу.
Примери узорка стандардне девијационе формуле (са Екцеловим предлошком)
Узмимо пример како бисмо боље разумели израчунавање узорка стандардног одступања.
Овде можете преузети овај узорак стандардног узорка стандардне одступања Формула Екцел овде - Пример узорка стандардног одступања формула Формуле ЕкцелУзорак стандардне формуле одступања - Пример бр. 1
Рецимо да имамо два узорка скупа података А&Б и сваки садржи 20 случајних података и имају исту средњу вредност. Израчунајте стандардно одступање узорка за скуп података А&Б.
Решење:
Просек се израчунава као:
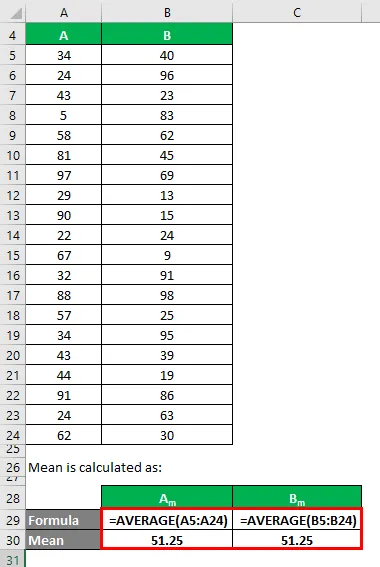
- Средња вредност скупа података А = 51.25
- Средња вредност скупа података Б = 51.25
Сада морамо израчунати разлику између података и средњих вредности.
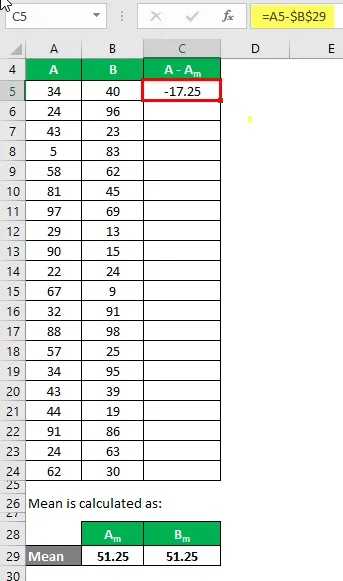
Слично томе, израчунајте за све скупове података А.
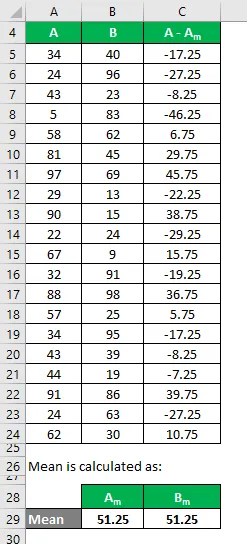
Слично томе, израчунајте и за скуп података Б.
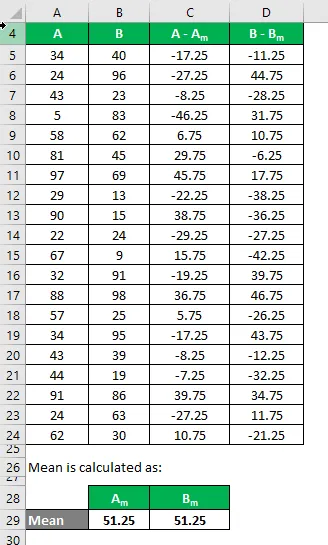
Израчунајте квадрат разлике за оба скупа података А и Б.
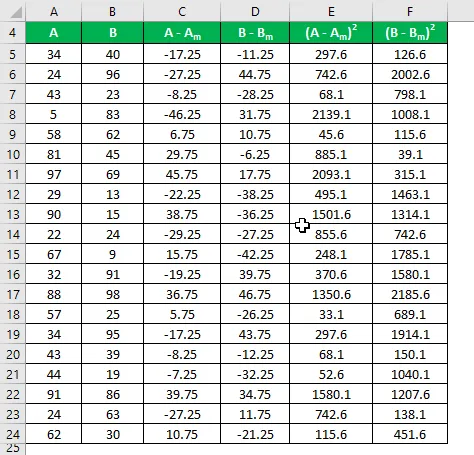
Узорак Стандардно одступање се израчунава помоћу доле наведене формуле
Узорак стандардног одступања = √ (Σ (Кс и - Кс м ) 2 / (н - 1))
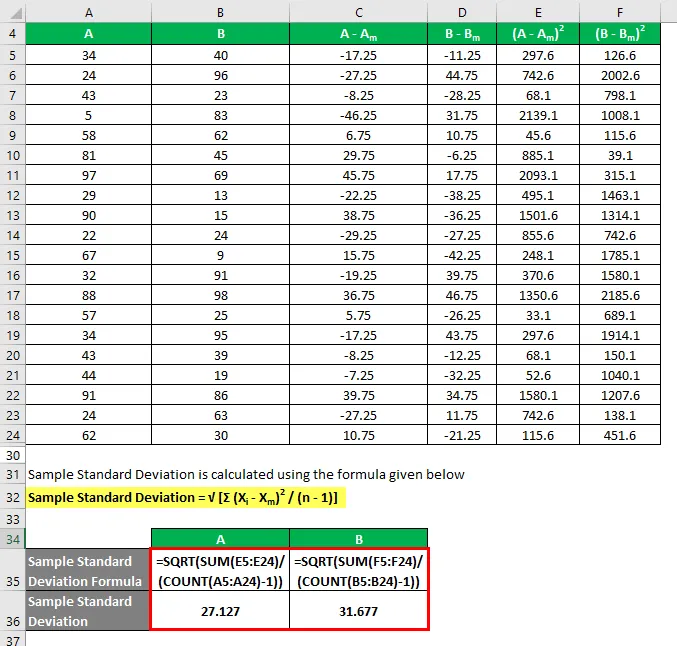
Дакле, ако овде видите, иако оба скупа података имају исту средњу вредност, Б има стандарднију девијацију од А, што значи да су тачке података од Б више дисперзиране од А.
Узорак стандардне формуле одступања - пример бр. 2
Рецимо да сте инвеститор веома ризичан и желите да уложите новац на берзу. Пошто је апетит за ризиком низак, желите да инвестирате у сигурне акције које имају нижи стандардни одклон. Ваш финансијски саветник предложио вам је 4 акције од којих можете да бирате. Желите да изаберете две залихе међу тих 4 и одлучићете то на основу ниже стандардне девијације.
Добили сте податке о њиховим историјским приносима за последњих 15 година.
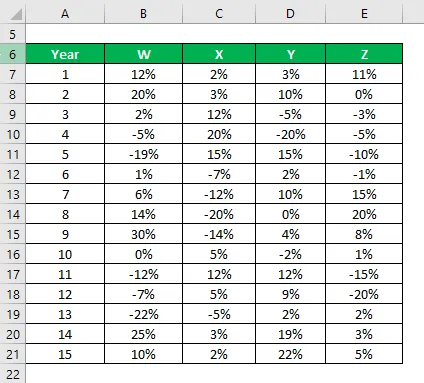
Решење:
Узорак стандардног одступања се израчунава помоћу екцел формуле
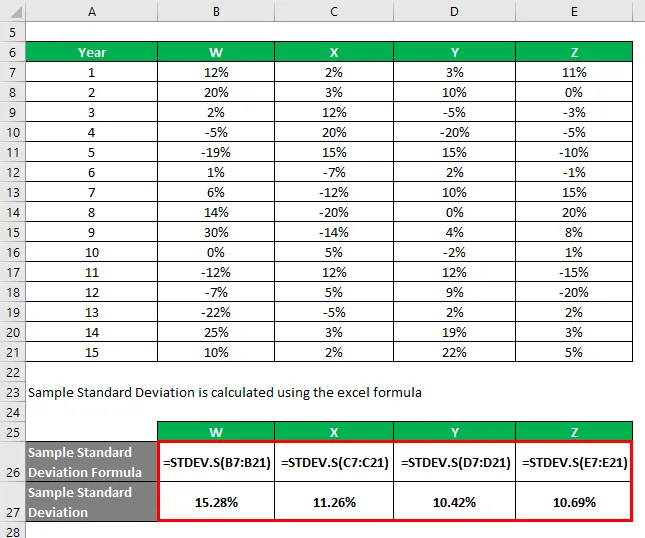
На основу података и стандардног одступања узорка, изабрати ћете залихе И и З за улагање јер имају најнижу стандардну девијацију.
Објашњење
Разговарамо о значењу стандардног одступања са статистичког становишта, али оно такође има виталну улогу ако говоримо о финансијској тачки гледишта. У финансијама је у основи мера ризика коју инвестиција носи и колико је ризична та инвестиција. На основу ризика који улагања имају, инвеститори могу затим израчунати минимални поврат који им је потребан да надокнаде тај ризик. Као што је у горњем примеру, будући да И и З имају мању стандардну девијацију, то значи да постоји мања варијабилност у враћању тих залиха, па су и мање ризичне. Једну тачку док користимо стандардни алат за одступање морамо имати на уму да су под великим утицајем екстремних вредности или одметника. Ови одласци могу да извргну стандардну вредност одступања.
Релевантност и употреба узорка стандардне формуле одступања
Стандардно одступање помаже инвеститорима и аналитичару да пронађу омјер ризика и награде или оштри омјер инвестиције. У основи, свако може зарадити стопа ризика без улагања, улажући у државне благајне и хартије од вредности без ризика. Али повратак изнад и изнад тога је вишак поврата и да бисте то постигли, оно што је ниво ризика који треба да преузмете је мјера оштрог омјера:
Оштар однос = (поврат инвестиције - стопа ризика без ризика) / стандардно одступање
Дакле, што је већи омјер Схарпе-а, боље је улагање.
Као што смо рекли да је стандардна девијација мерило ризика, али нижа вредност стандардне девијације није увек пожељна. Ако инвеститор има већи апетит за ризиком и жели да улаже агресивније, биће вољан да преузме више ризика и преферира релативно веће стандардно одступање од инвеститора који спречава ризик. Дакле, све зависи од нивоа ризика који је инвеститор спреман да преузме.
Препоручени чланци
Ово је водич за узорак Формуле стандардне одступања. Овде смо расправљали о томе како израчунати узорак стандардног одступања заједно са практичним примерима и довнлоад-ом Екцел шаблона. Такође можете погледати следеће чланке да бисте сазнали више -
- Примери формуле варијансе популације
- Калкулатор за релативно стандардно одступање
- Како израчунати стандардну нормалну дистрибуцију?
- Прорачун биномне дистрибуције