Вектори у Матлабу - Врсте векторског рада са примерима

Увод у векторе у Матлабу

Вектор је приложени скуп елемената. У Матлабу можемо да створимо векторе користећи квадратне заграде. Вектори су једна од илустрација низова (једнодимензионални низ). може се представити на два начина вектор реда и ступаца.

Ред Вецтор

То је хоризонтални скуп елемената. Представља се унутар квадратних заграда. Сваки елемент је одвојен зарезом или размаком.

Кс = (4 7 8) или Кс = (4, 7, 8)

Цолумн Вецтор

То је вертикални скуп елемената. Такође је представљен унутар углатих заграда. Прво постоје два начина за креирање вектора колона: одвајањем сваког елемента зарезом и другим начином писања сваког елемента у следећем реду у наредбеном прозору.

Кс = (4; 6; 7) или

Кс = (4)

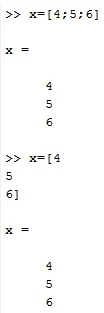
Векторске операције

Векторски оператери су широко класификовани у две категорије.

1. Аритметичка операција

Размотримо два вектора к и и са вредностима к = (1 4 5 3) и и = (5 3 2 1), а на ова два вектора к и и можемо извести различите операције.

а. Умножавање: Ова функција се користи за умножавање било које аритметичке вредности на цео вектор.

На пример:

мул = 3 * к

мул = 3 * (1 4 5 3)

мул = (3 12 15 9)

Синтакса: variable name = arithmetic constant * vector name

б. Тригонометријска функција: Можемо применити било коју тригонометријску функцију на векторском греху, цос, тан, цосец, сец, итд.

Пример три = цос (к)

Одговор је: 0, 54 - 0, 65 0, 28 -0, 99

Синтакса: variable name = trigonometric function name ( vector name )

Збир: Ово показује укупно (додавање) целих елемената у једном вектору.

Пример

к = (1 4 5 3)

Укупно = сума (к)

Излаз је укупан = 13

Синтакса: variable name = = sum ( vector name )

ц. Дужина: Приказује дужину одређеног вектора, нека нам буде један вектор п = (9 7 5 3 1 9 7 5 3 1)

Пример

п = (9 7 5 3 1 9 7 5 3 1)

Лен = дужина (п)

Излаз је Лен = 10

д. Додавање вектора: Додавање два или више вектора је једноставан рад у Матлабу, размотримо два вектора п и к.

П = (4 6 3 2) и к = (5 7 9 1)

Додајте = п + к

Излаз је Додај = (9 13 12 3)

Синтакса: vector name operator ( + ) vector name

Слично томе, можемо да радимо и одузимање, као што је суб = п - к

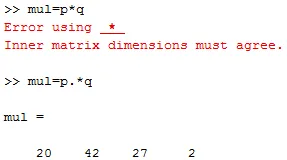
е. Умножавање вектора : Ако желимо да множимо два вектора, тада једноставан оператор множења (*) неће радити. Стога морамо додати оператора тачака ('.') Са оператором множења.

Пример:

П = (4 6 3 2) и к = (5 7 9 1)

мул = п. * к

излаз је мул = (20 42 27 2)

Синтакса: variable name = vector name dot operator multiplication operator vector name

Претпоставимо да желим сазнати квадрат једног одређеног вектора или желим да вектор умножим само са тим вектором.

Тада ће синтакса бити скур = к. 2

2. Релацијско управљање

а. Једнако је оператору : овај оператор упоређује сваки н сваки елемент из два вектора и даје излаз једнак нули и један облик.

Пример

м = (2 5 8)

И н = (5 5 3)

Као што знамо да постоје три елемента у вектору м и вектору н,

м == н

Горња изјава даје излаз као 0 1 0, што значи да прво не није једнако, други број је једнак а трећи не није једнак. О представља лаж и 1 представља тачно.

б. Мање од оператера (<): Мање него што оператор представља симболом '<'. можемо да упоредимо дату матрицу са било којом аритметичком константом или са било којим другим вектором.

Пример

м = (3 2 4)

н = (1 1 1)

м <н

излаз ће бити 0 0 0, што значи да су сви бројеви већи од вектора н.

и ако је м <10

тада ће излаз бити 1 1 1, што значи да су сви бројеви мањи од 10.

ц. Већи од оператера (>): Већи него што оператор представља симболом ('>'). Дату матрицу можемо упоредити са било којом аритметичком константом или било којим другим вектором.

Пример:

М = (3 2 4)

Н = (1 1 1)

м> н

Излаз ће бити 1 1 1, што значи да су све вредности веће од вредности вектора н.

Закључак - Вектори у Матлабу

У Матлабу можемо створити различите типове вектора где можемо изводити различите операције попут сабирања, одузимања, множења, квадрата, квадратног корена, снаге, скалирања, векторског множења, тачканог производа итд.

Препоручени чланци

Ово је водич за Векторе у Матлабу. Овде смо размотрили врсте векторских операција које укључују аритметичку и релацијску операцију заједно са неким примерима. Такође можете погледати следеће чланке да бисте сазнали више -